Introduction
RoPE 已经成为了大多数 LLM 使用的 position encoding 范式,但是,RoPE 与 LLM long context 之间的关系还没有被探索清楚。在本文中,作者就探究了 base frequency 与 LLM context capability 之间的关系,并给出了一个达到指定上下文长度所需要的 base frequency 的 lower bound.
Method
首先作者回顾了 attention 与 RoPE 的定义, 关键就是 RoPE 这部分,如下所示
$$ A_{ij} = (R_{i,\theta}q_i)^T(R_{j,\theta}k_j) = q_i^TR_{i-j,\theta}k_j $$这里 $\theta$ 就是 base frequency, 作者总结不同模型的 base frequency 配置如下表所示
| Model | Llama-7B | Llama2-7B | Llama3-8B | Mistral-7B | Baichuan2-7B |
|---|---|---|---|---|---|
| Base frequency | 10,000 | 10,000 | 500,000 | 1,000,000 | 10,000 |
| Context length | 2048 | 4096 | 8192 | 32,768 | 4,096 |
接下来,作者回顾了 YARN. 其核心思想在于,预训练阶段所有可能的 $\cos(t-s)\theta_i$ 都见过,才能保证模型的 OOD 表现
作者认为 base frequency 的设置应该满足两个条件:
- The closer token gets more attention: 当前的 token 应该给邻近的 token 更高的注意力
- The similar token gets more attention: 当前的 token 应该给相似的 token 更高的注意力
在 RoPE 中,作者已经给出了 $A_{ij}$ 与相对距离 $|i-j|$ 之间的关系。因此第一个性质已经满足了。
接下来,作者分析了相似 token 的性质,作者定义 token 的相似性如下:
$$ \mathbb{E}_{q,k^*}[q^TR_{m,\theta}k^*] - \mathbb{E}_{q,k}[q^TR_{m,\theta}k] $$这里 $k^*=q+\epsilon$ 代表了相似的 token, 而 $k$ 是一个随机 token. 作者给出的结论如下
Theorem 假设 $q,k\in\mathbb{R}^d$ 独立同分布,它们的标准差为 $\sigma\in\mathbb{R}$, 则对于 $k^*=q+\epsilon$, $\epsilon$ 是一个随机变量满足 $\mathbb{E}[\epsilon]=0$, 则我们有
$$ \mathbb{E}_{q,k^*}[q^TR_{m,\theta}k^*] - \mathbb{E}_{q,k}[q^TR_{m,\theta}k] = 2\sigma^2\sum_{i=0}^{d/2-1}\cos(m\theta_i) $$作者定义 $B_{m,\theta}=\sum_{i=0}^{d/2-1}\cos(m\theta_i)$, 作者认为给定 $\theta$, 模型的上下文长度 $L_\theta$ 满足
$$ L_\theta = \sup\{L\mid B_{m,\theta}\geq 0, \forall m\in[L]\} $$也就是说,base frequency 决定了 LLM 的上下文长度。作者给出了不同的上下文长度对应的 base frequency 如下表所示
| Context Len. | 1k | 2k | 4k | 8k | 16k | 32k | 64k | 128k | 256k | 512k | 1M |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower Bound | 4.3e3 | 1.6e4 | 2.7e4 | 8.4e4 | 3.1e5 | 6.4e5 | 2.1e6 | 7.8e6 | 3.6e7 | 6.4e7 | 5.1e8 |
总的来说,远距离衰减性保证了模型会更关注邻近的 token, 而相似 token 保证了模型能够区分出真正有意义的 token.
Experiments
作者首先分析了 base frequency 在 fine-tuning 阶段对模型上下文能力的影响,实验结果如下图所示
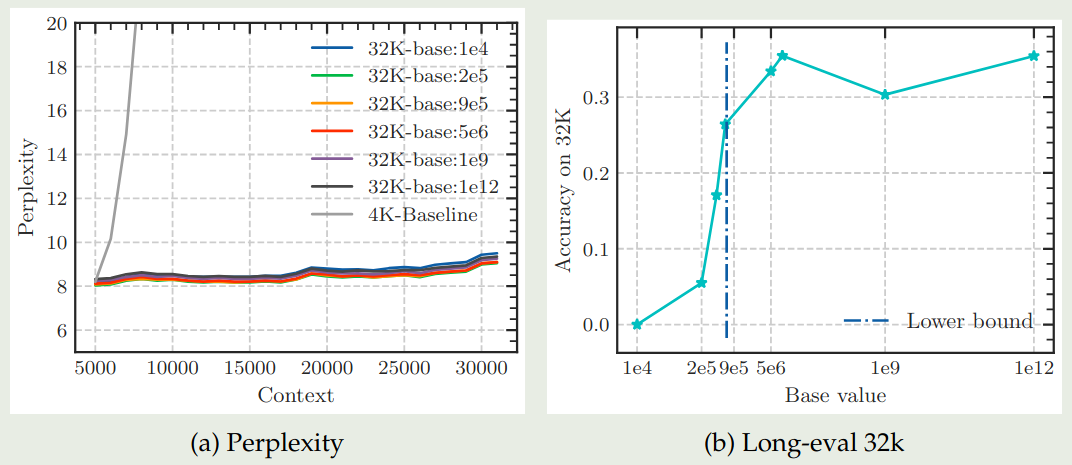
从实验结果可以看到,当 base frequency 低于阈值时,模型的表现急剧下降。
作者进一步探讨了 base frequency 对于模型 pre-training 阶段的影响,结果也是一样的,即非常小的 base frequency 会限制模型的 context 能力,结果下图所示 (三行分别代表了 base frequency 为 1e2, 1e4 和 1e6 的情况)
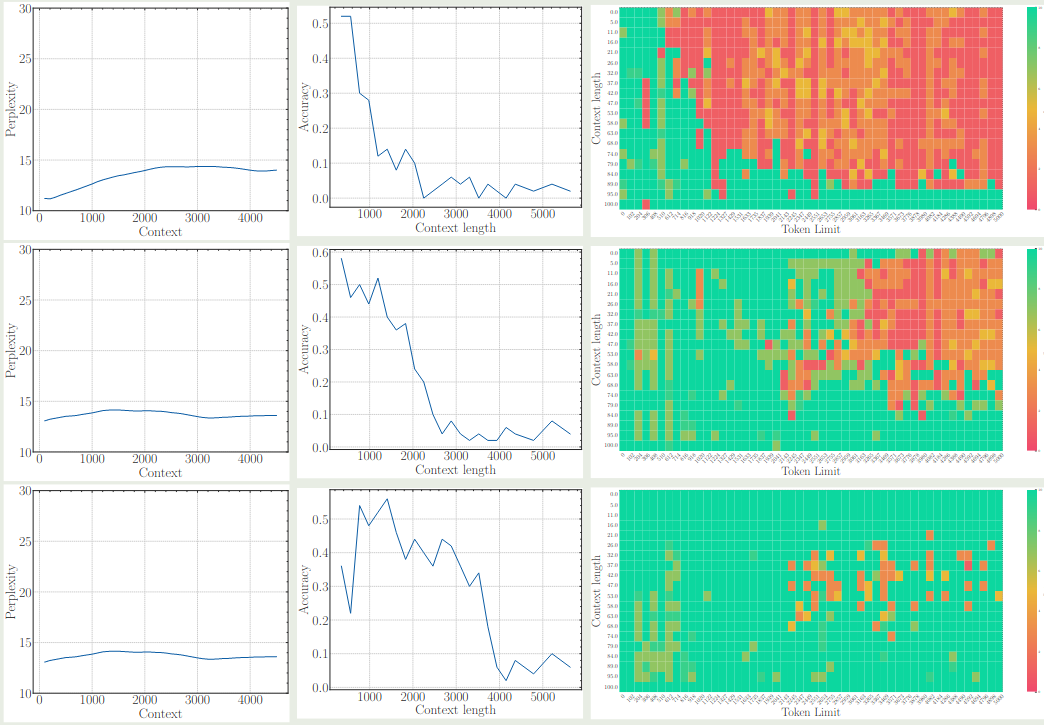
可以看到,尽管 perplexity 都差不多,但是使用更大的 base frequency 其长上下文能力明显更好。
作者进一步分析了为什么较小的 base frequency 会影响模型的长上下文能力。作者认为较小的 base frequency 会导致 $B_{m,\theta}$ 接近于 0, 从而模型难以区分随机 token 和相似 token, 这样模型只能依赖于邻近 token 进行学习,这样就限制了模型的长上下文能力
作者还进一步对比了提高 base frequency 与 Interpolation 两种做法,实验结果如下表所示
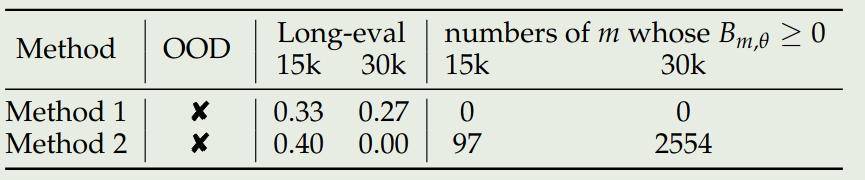
实验结果说明,Interpolation 在上下文超过 30K 之后,其 $B_{m,\theta}\leq0$ 的 次数显著增加,表明了其和上下文能力之间的关系。
Conclusion
作者在本文中,探究了 RoPE 中 base frequency 与 LLM 上下文能力之间的关系,发现了提高模型的上下文能力需要关注 RoPE 的 base frequency 超参数,并给出了对应的 lower bound. 作者通过实验验证了这个观点。