DeepSeek 在 2024 年 1 月 5 日发布了 DeepSeek LLM, 包括 7B 和 67B 两个 size, 作者主要强调了对于 scaling law 的探究
Introduction
已有的 scaling law 如 Kaplan 和 Chinchilla 介绍了 model size, dataset size, compute budget 与模型表现之间的关系。在本文中,作者进一步探究了 learning rate 和 batch size 等超参数与模型表现之间的关系。基于发现的 scaling law, 作者为不同大小的模型设置了最优的超参数。并且,作者还发现不同数据集与模型表现之间的关系。
最终,基于这些实验结果,作者提出了 DeepSeek LLM, 模型使用 2T token 进行预训练,使用 1M samples 进行后训练,后训练包括 SFT 以及 DPO.
Pre-training
Architecture
DeepSeek-LLM 的架构与 LLaMA 基本相同,作者在 67B 的模型上使用了 GQA 来提高 inference 效率。最终模型的配置如下表所示
| Params | 7B | 67B |
|---|---|---|
| $n_{\text{layers}}$ | $30$ | $95$ |
| $d_{\text{model}}$ | $4096$ | $8192$ |
| $n_{\text{heads}}$ | $32$ | $64$ |
| $n_{\text{kv\_heads}}$ | $32$ | $8$ |
| Context Length | $4096$ | $4096$ |
| Sequence Batch Size | $2304$ | $4608$ |
| Learning Rate | $4.2e-4$ | $3.2e-4$ |
| Tokens | 2T | 2T |
Data
作者主要从 Common Crawl 构建预训练数据,数据处理过程包括:去重,过滤以及 remixing 三个步骤。
对于 tokenizer, 作者使用了 BBPE 算法,tokenizer 的大小设置为 100,000, 最终的 tokenizer 大小为 102400.
Hyper Parameters
作者主要对比了一下不同 learning rate schedule 的表现:
- cosine learning schedule
- multi-step learning rate schedule: 包含三个 Stage, 第一个 stage 保持最大学习率,第二个 stage 将学习率降低为最大学习率的 $31.6\%$, 第三个 stage 降低为最大学习率的 $10\%$.
对比的实验结果如下图所示
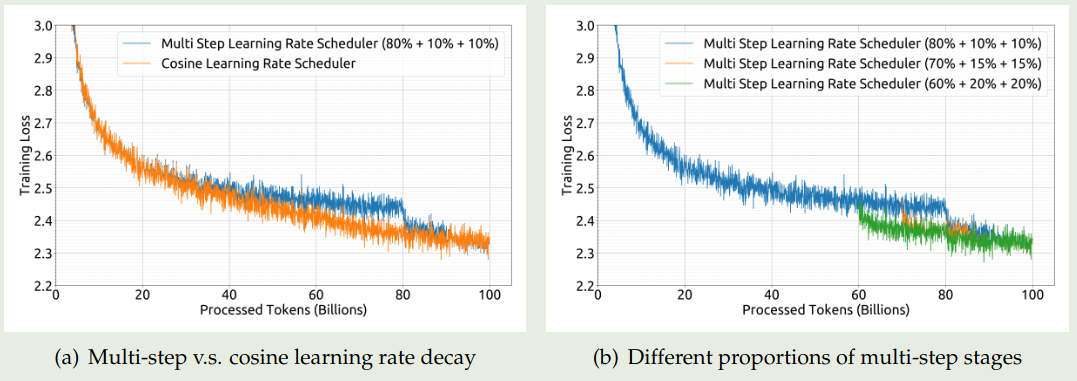
实验结果显示,multi-step learning rate scheduler 的表现与 cosine learning rate 表现差不多。并且,multi-step learning rate scheduler 对于 continue pretraining 支持更好。因此在本文中作者使用了 multi-step learning rate scheduler.
Infra
作者使用了数据并行,张量并行,序列并行以及 1F1B pipeline 并行。作者还使用了 flash attention 来提高硬件利用率。
Scaling Law
本节中,作者分析了 scaling law, 主要有以下三点:
- 构建了针对 learning rate 和 batch size 的 scaling law
- 作者使用 non-embedding FLOPs/token $M$ 来表示 model scale
- 预训练数据的质量对最后中的 scaling 影响很大
作者首先构建了针对 batch size 和 learning rate 的 scaling law, 结果显示最优的 learning rate 和 batch size 范围都比较广,这个结论与 Kaplan 一致。
接下来,作者构建了 batch size $B$, learning rate $\eta$ 与 compute budget $C 之间的关系,实验结果如下图所示
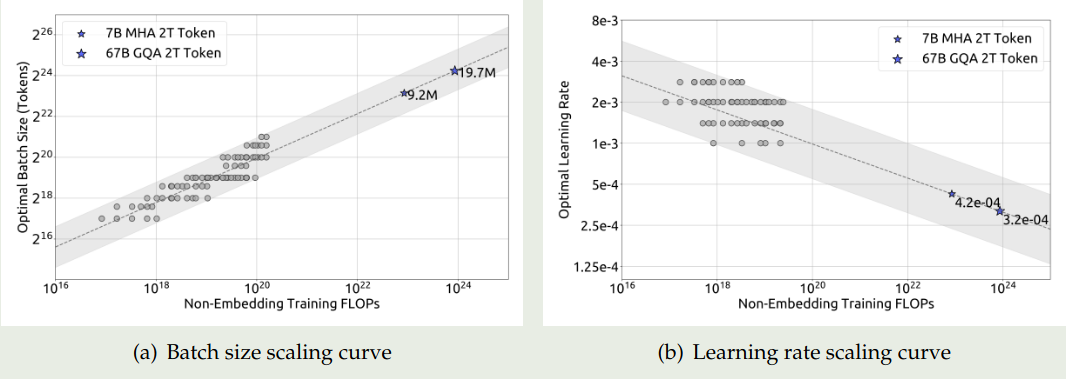
拟合得到的曲线为
$$ \begin{aligned} \eta_{opt} &= 0.3118* C^{-0.1250}\\ B_{opt} &= 0.2920 * C^{0.3271} \end{aligned} $$可以看到,随着 compute budget 增加,$B_{opt}$ 也逐渐增加,而 $\eta_{opt}$ 逐渐减小。并且,最优参数的范围都比较广。
接下来,作者进一步探究了 batch size 与 generalization error $L$ 之间的关系。作者希望找到 model scale $N$, data scale $D$ 与 compute budget $C$ 之间的关系,即
$$ N_{opt} \varpropto C^a,D_{opt} \varpropto C^b $$compute budget 与 model scale, data scale 之间的关系可以近似表示为 $C=6ND$, 这个公式的推导见 LLM FLOPs computation。我们用 $N_1,N_2$ 分别表示模型的 non-embedding parameter 以及 complete parameters, 则我们可以用 $6N_1$ 或者 $6N_2$ 来近似 model scale, 但是 $6N_1$ 和 $6N_2$ 均没有考虑 attention 的计算开销,因此这两种近似的误差都比较大。
为了解决这个问题,作者提出了一个新的 model scale 表示形式,即 non-embedding FLOPS/token $M$, 其中 $M$ 包含 attention 的计算开销但是不包含 vocabulary computation. 基于这种表示,compute budget 可以近似表示为 $C=MD$. $M$ 与 $6N_1,6N_2$ 的区别表示如下所示
$$ \begin{aligned} 6N_1 &= 72nd^2\\ 6N_2 &= 72nd^2 + 6Vd\\ M &= 72nd^2+12ndl \end{aligned} $$其中, $d$ 是 hidden size, $n$ 是 layers 个数, $V$ 是 vocabulary size, $l$ 是 sequence length. 作者在不同 scale 的模型上比较了三种表示方式,结果发现 $6N_1$ 和 $6N_2$ 要么低估,要么高估了模型的参数量。
基于 model scale 的表示方式,作者构建了如下的优化问题
$$ M_{opt}(C), D_{opt}(C) = {\arg\min}_{M,D\ s.t.\ C=MD} L(N,D) $$作者使用了 Chinchilla 提出来的 IsoFLOP 曲线进行拟合,实验结果如下图所示
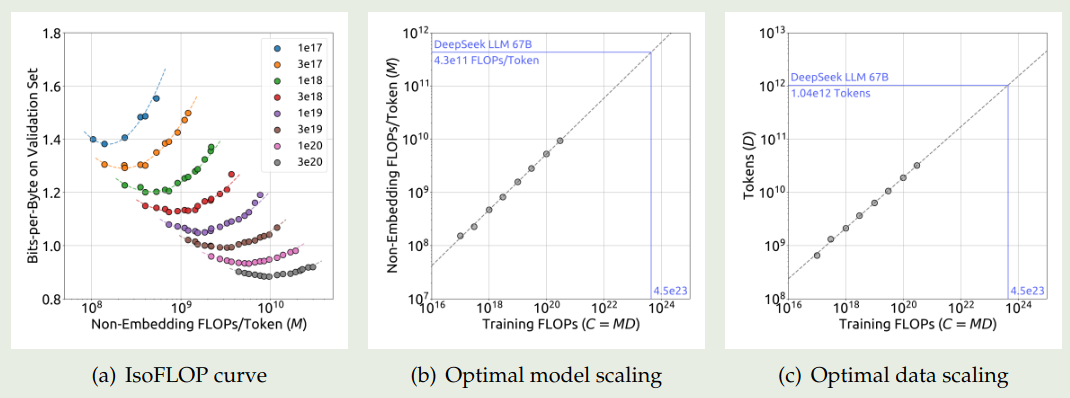
拟合的曲线为
$$ M_{opt}(C) = 0.1715*C^{0.5243}, D_{opt}(C) = 5.8316*C^{0.4757} $$作者还进一步拟合了 compute budget 与 optimal generalization error 之间的关系,结果如下图所示
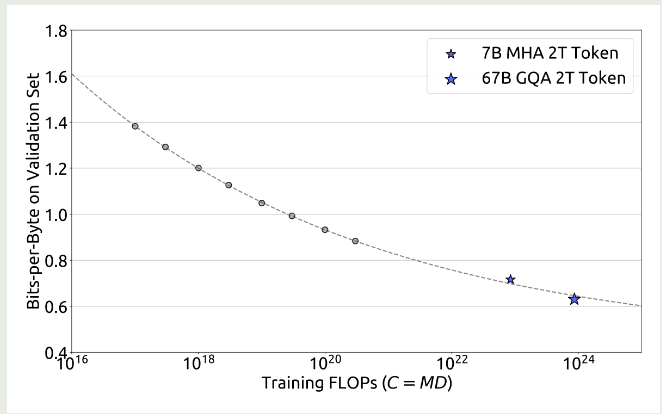
实验结果显示,作者提出的 scaling law 可以很好预测模型的表现。
最后,作者探究了以下不同数据集的 scaling law, 作者使用 early in-house data, current in-house data 以及 OpenWebText2 来将进行实验,结果如下图所示
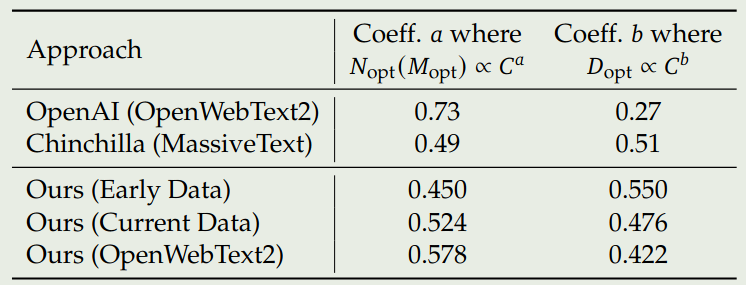
结果显示,scaling law 与数据质量高度相关。当数据质量提升时,model scaling exponent $a$ 逐步提升,data scaling exponent $b$ 逐步下降,说明 compute budget 更多由模型参数量决定。因此,作者认为提升 compute budget 之后,我们应该优先提高模型的 model size.
Post-training
作者构建了 1.5M 的中英文指令数据。其中安全性的数据有 300K, 有帮助性的数据有 1.2M, 其中包括 $31.2\%$ 的通用数据,$46.6\%$ 的数学相关数据,$22.2\%$ 的代码数据。
post-training 包含两个阶段:
- SFT:7B 的模型训练了 4 个 epoch, 67B 的模型训练了 2 个 epoch, 作者发信进一步训练 67B 的模型会导致过拟合。作者发现,模型在训练过程中会出现重复输出的情况,特别是数学 SFT 数据,为了解决这个问题,作者使用了一个两阶段的 SFT 以及 DPO.
- DPO: 提高模型的能力,作者发现 DPO 可以提高模型 open-ended generation skill.
Evaluation
我们主要关注一下消融实验。
首先作者探究了分阶段 SFT 对模型表现的影响。作者发现,小模型在 math 和 code 数据集上需要训练更长时间,但是这也损害了模型的对话能力。为了解决这个问题,作者使用两阶段的训练模式,第一个阶段使用所有的数据进行训练,第二个阶段仅使用对话数据进行训练,实验结果如下表所示
| Model | HumanEval | GSM8K | Repetition | IFEval |
|---|---|---|---|---|
| DeepSeek LLM 7B Chat Stage1 | 48.2 | 63.9 | 0.020 | 38.0 |
| DeepSeek LLM 7B Chat Stage2 | 48.2 | 63.0 | 0.014 | 41.2 |
可以看到,经过第二阶段训练之后,模型的表现有所提升
接下来,作者探究了 Multi-choice question 对模型表现的影响,MCQ 要求模型不仅需要有相关的知识,还要理解每个选项的含义。作者使用 20M 中文 MCQ 来进行消融实验,结果如下表所示
| Model | MMLU | CEval | CMMLU | TriviaQA | ChineseQA | |
|---|---|---|---|---|---|---|
| DeepSeek LLM 7B Chat | 49.4 | 47.0 | 49.7 | 57.9 | 75.0 | |
| DeepSeek LLM 7B Chat + MC | 60.9 | 71.3 | 73.8 | 57.9 | 74.4 |
实验结果显示,MCQ 确实可以提高模型在上述几个 benchmark 上的表现,但是其泛化性会下降。因此,作者在 pre-training 和 fine-tuning 阶段并没有使用 MCQ 数据进行训练。
作者还探究了在 pre-training 阶段加入 instruction data, 来提高 base model 在下游 benchmark 上的表现。结果发现,base model 的表现提升优先。作者认为,尽管 instruction data 可以提高 base model 表现,但是如果 Instruction data 数量过少,则模型表现不太可能学习到有用的知识。因此,作者的做法是不在 pretraining 阶段加入 Instruction data.
最后,作者探究了 system prompt 对模型表现的影响。受 LLaMA 2 启发,作者也尝试在输入中加入 system prompt. 实验结果如下所示
| Model | MT Bench |
|---|---|
| DeepSeek LLM 7B Chat | 7.15 |
| DeepSeek LLM 7B Chat + System Prompt | 7.11 |
| DeepSeek LLM 67B Chat | 8.35 |
| DeepSeek LLM 67B Chat + System Prompt | 8.58 |
可以看到,7B 的模型加入 system prompt 之后,模型表现有所下降;67B 的模型加入 system prompt 之后,模型表现有所提升。作者认为,大模型更容易理解 system prompt 的意图,而小模型的指令跟随能力则较差,因此 system prompt 反而会影响模型表现。
Conclusion
作者在本文中提出了 DeepSeek LLM 系列大语言模型,作者详细介绍了超参数的选择以及 scaling law 等。