DeepSeek 在 2024 年 1 月发布了 DeepSeekMoE, 一个解决 MoE 模型 specialization 不足以及 redundancy 问题的大模型系列。
Introduction
作者首先回顾了已有 MoE 模型的不足,主要有两点:
- knowledge hybridity: 已有 MoE 模型的专家个数比较少,这就导致每个专家需要掌握更多样化的知识,提高了训练难度
- knowledge redundancy: 不同专家掌握的知识可能有重叠,从而导致了模型参数的 redundancy
为了解决这两个问题,作者提出了 DeepSeek-MoE, DeepSeek-MoE 主要做出了两点改变:
- Fine-Grained Expert Segmentation: 作者使用了更多的专家,来提高每个专家的 specialization, 降低训练成本
- Shared Expert Isolation: 作者在 Routing expert 的基础上,加入了 shared expert 来学习 common knowledge.
作者在 2B-A0.6B 的模型进行了实验,结果显示模型表现超过了 GShard, 说明了 DeepSeekMoE 模型架构的有效性。
作者还进一步将模型 scale 到了 16B-A2.8B 和 145B-A22B, 实验结果均验证了模型的 scaling 效果。
Method
Preliminary
作者首先回顾了 transformer 架构,transformer 的第 $\ell$ 层 decode layer 可以表示为
$$ \begin{aligned} u_{1:T}^{\ell} &= \mathrm{self\_attention}(h_{1:T}^{\ell-1}) + h_{1:T}^{\ell}\\ h_t^\ell &= \mathrm{FFN}(u_t^{\ell}) + u_t^{\ell} \end{aligned} $$其中 $T$ 是 sequence length, $h_{1:T}^{\ell-1}$ 是第 $\ell-1$ 层 decoder layer 输出的 hidden states.
接下来,我们可以将 dense 架构转换为 MoE 架构,MoE 架构与 dense 架构不同的地方在与 $\mathrm{FFN}$ 不再是 MLP, 而是一个 MoE 模块,其表达式如下
$$ \begin{aligned} h_t^\ell &= \sum_{i=1}^N\left(g_{i,t}\mathrm{FFN}_i(u_t^{\ell})\right) + u_t^{\ell}\\ g_{i,t} &= \begin{cases} s_{i,t,}, &s_{i,t}\in\mathrm{Topk}(\{s_{j,t}\mid 1\leq j \leq N\},K)\\ 0, &\text{otherwise} \end{cases}\\ s_{i,t,} &= \mathrm{softmax}_i({u_t^{\ell}}^Te_i^{\ell}) \end{aligned} $$这里 $N$ 是专家的总个数, $K$ 是激活专家个数, $e_{i}^{\ell}$ 是 routing layer 的权重矩阵,$\mathrm{FFN}_i$ 是每个专家对应的 FFN.
DeepSeekMoE Architecutre
DeepSeekMoE 架构如下图所示
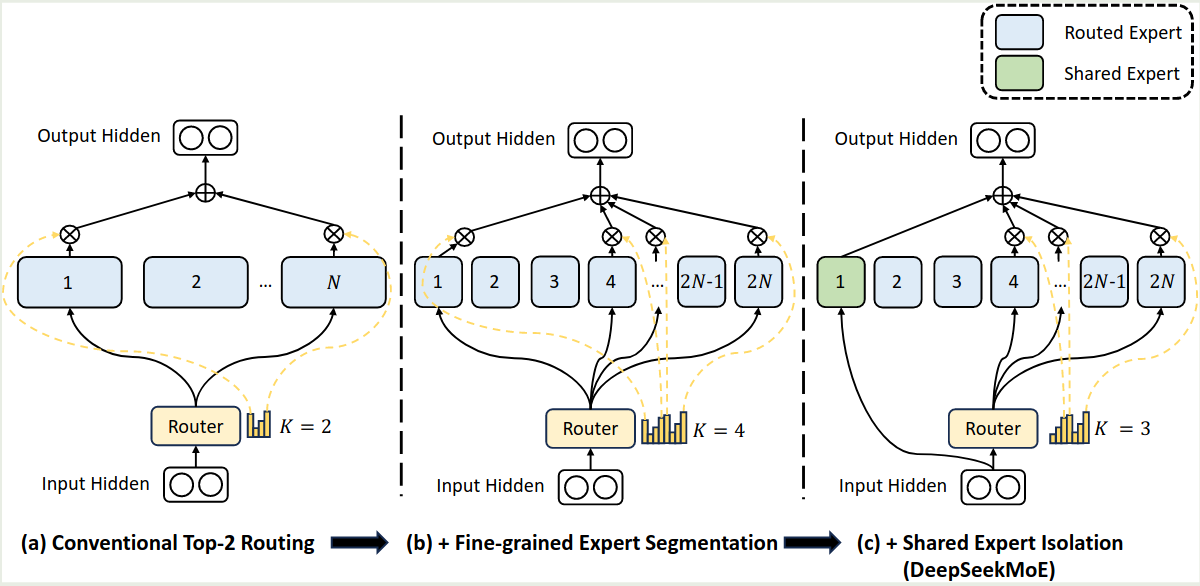
相比于其他 MoE 架构,DeepSeekMoE 主要做了以下几点改变。
Fine-Grained Expert Segmentation
作者首先解决了每个专家学习内容过多的问题。作者的做法就是将每个 expert FFN 分割为 $m$ 个更小的专家,具体做法就是将 FFN intermediate hidden size 降低为原来的 $1/m$. 这样的话就可以在不增加模型参数量的情况下提高模型的表现。修正后的 MoE 模块为
$$ \begin{aligned} h_t^\ell &= \sum_{i=1}^{mN}\left(g_{i,t}\mathrm{FFN}_i(u_t^{\ell})\right) + u_t^{\ell}\\ g_{i,t} &= \begin{cases} s_{i,t,}, &s_{i,t}\in\mathrm{Topk}(\{s_{j,t}\mid 1\leq j \leq mN\},mK)\\ 0, &\text{otherwise} \end{cases}\\ s_{i,t,} &= \mathrm{softmax}_i({u_t^{\ell}}^Te_i^{\ell}) \end{aligned} $$可以看到,现在我们一共有 $mN$ 个专家,激活专家个数为 $mK$ 个。作者认为,通过提高专家的粒度,我们可以有效增加专家组合的可能性,这就提高了最终的组合多样性。
Shared Expert Isolation
接下来,作者介绍了解决不同专家学习到重复知识的问题,作者的做法是在 routing Expert 的基础上加入 Shared expert. 也就是说,有固定几个专家始终都会被激活,这部分专家复杂学习通用知识,从而减少知识冗余。增加 shared expert 之后的 MoE 模块为
$$ \begin{aligned} h_t^\ell &= \sum_{i=1}^{K_s}\mathrm{FFN}_i(u_t^{\ell})+\sum_{i=K_s+1}^{mN}\left(g_{i,t}\mathrm{FFN}_i(u_t^{\ell})\right) + u_t^{\ell}\\ g_{i,t} &= \begin{cases} s_{i,t,}, &s_{i,t}\in\mathrm{Topk}(\{s_{j,t}\mid K_s+1\leq j \leq mN\},mK-K_s)\\ 0, &\text{otherwise} \end{cases}\\ s_{i,t,} &= \mathrm{softmax}_i({u_t^{\ell}}^Te_i^{\ell}) \end{aligned} $$此时,模型中一共包含 $K_s$ 个共享专家,$mN-K_s$ 个 routing expert, 其中激活专家个数为 $mK-K_s$.
Load Balancing Loss
接下来,作者解决了训练时的 load imbalance 问题,作者提出了两个 loss 来分别解决不同层面的 load imbalance 问题。
首先,在 expert 层面,作者使用了如下的 load balancing loss:
$$ \mathcal{L} = \alpha_1\sum_{i=1}^{N'}f_iP_i $$其中 $\alpha_1$ 是超参数,
$$ f_i = \frac{N'}{K'T}\sum_{i=1}^{N'}\mathbb{1}(\text{Token }i \text{ selects Expert }i),\quad P_i = \frac{1}{T}\sum_{t=1}^Ts_{i,t} $$分别为以及分配给第 $i$ 个专家的 token 比例以及概率之和。$N'=mN-K_s$, $K'=mK-K_s$. $\mathbb{1}(\cdot)$ 是 indicator function.
其次,在 device 层面,作者也是用了 load balancing loss 来减少不同设备之间不必要的通信。作者将 routed experts 分为 $D$ 个 group $\mathcal{E}_1,\dots,\mathcal{E}_D$, 然后每个设备部署一个 group, group level 的 load balancing loss 定义如下:
$$ \mathcal{L} = \alpha_2\sum_{i=1}^D f_i' P_i' $$其中 $\alpha_2$ 是超参数,
$$ f_i' = \frac{1}{|\mathcal{E}_i|}\sum_{j\in\mathcal{E}_i}f_i,\quad P_i' = \sum_{j\in\mathcal{E}_i}P_i $$实际中,作者使用了一个较小的 $\alpha_1$ 来避免 routing collapse, 使用了一个较大的 $\alpha_2$ 来提高 Device 层面的负载均衡。
Training
作者使用了中英文数据进行训练,tokenizer 基于 BPE 算法,vocab size 为 8K. 模型训练基于 HAI-LLM.训练时使用了 TP, DP, PP, EP 等并行策略。
2B, 16B, 145B 模型的参数如下表所示
| Model | 2B | 16B | 145B |
|---|---|---|---|
| total params | 2B | 16.4B | 144.6B |
| activated params | 0.3B | 2.8B | 22.2B |
| hidden size | 1280 | 2048 | 4096 |
| layers | 9 | 28 | 62 |
| attention heads | 10 | 16 | 32 |
| head dimension | 128 | 128 | 128 |
| routed experts | 63 | 64 | 128 |
| activated experts | 7 | 6 | 12 |
| shared experts | 1 | 2 | 4 |
| training tokens | 100B | 2T | 245B |
Experiments
Alignment
作者针对 DeepseekMoE 16B 进行了微调,微调使用了 1.4M 的训练样本,覆盖了 math, code, QA, reasoning 等任务。
Ablation Study
作者在 2B 的模型上进行了 ablation study.
首先,作者探究了细粒度专家和共享专家的有效性,结果如下图所示
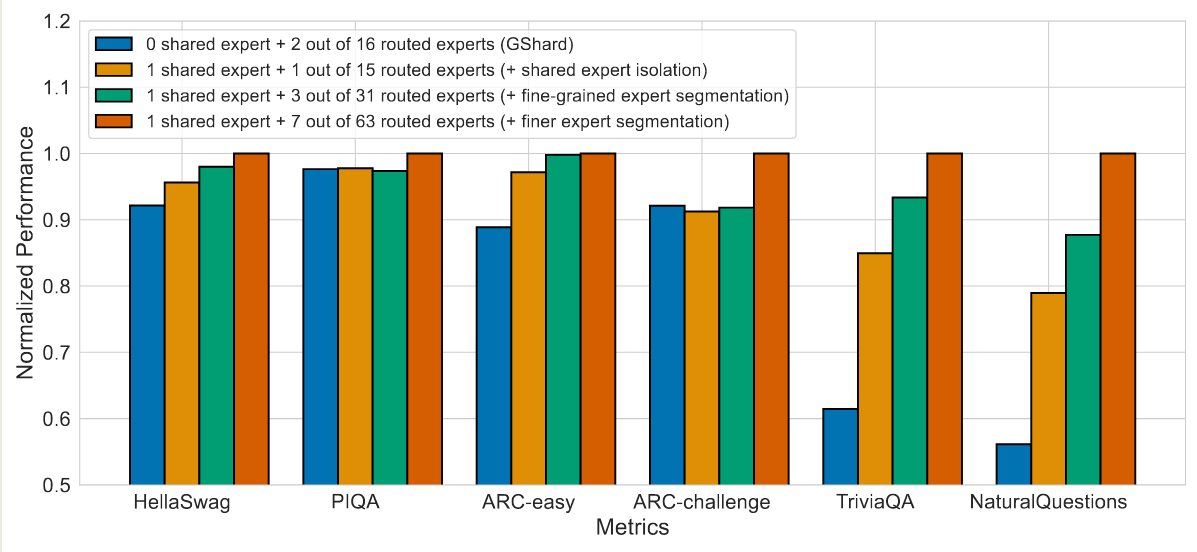
实验结果显示,与 GShard 相比,使用共享专家可以有效提高模型的表现。并且,使用更细粒度的专家也可以进一步提高模型的表现
作者还探究了共享专家与路由专家的比例,作者分别使用不同的比例进行实验,结果发现共享专家:路由专家个数为 1:3 的时候模型效果最好。
作者还探究了模型的泛化性,作者 mask 掉一部分概率最高的 routing expert, 然后从剩下的专家里进行 topK 的挑选,然后作者比较模型和 GShard 的表现,结果如下图所示
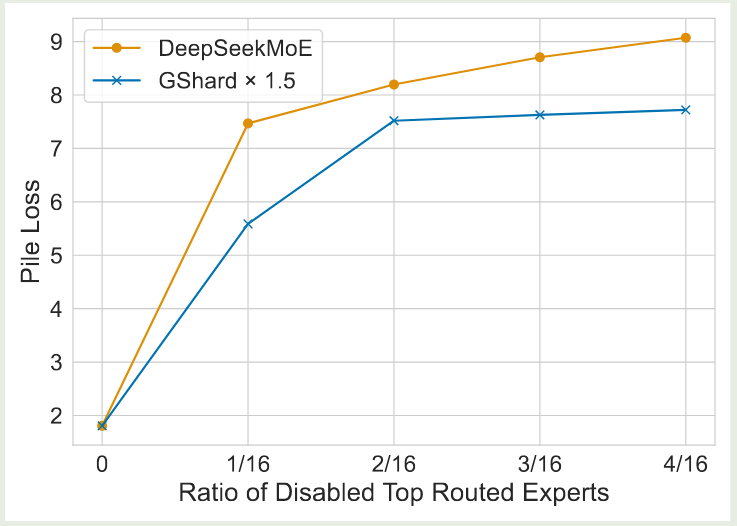
实验结果显示,DeepSeekMoE 对于 mask 操作更敏感,这说明 DeepSeekMoE 模型中专家的 specialization 更强。
作者还探究了 mask 掉共享专家对模型表现的影响,结果显示共享专家与路由专家之间的 overlap 很小,去掉共享专家之后,模型表现会变差。
作者进一步分析了共享专家与路由专家组合的有效性。作者探究 DeepSeekMoE 是否可以使用更少的路由专家来获取知识。作者通过使用不同的 activated routed experts 来进行实验,实验结果如下图所示
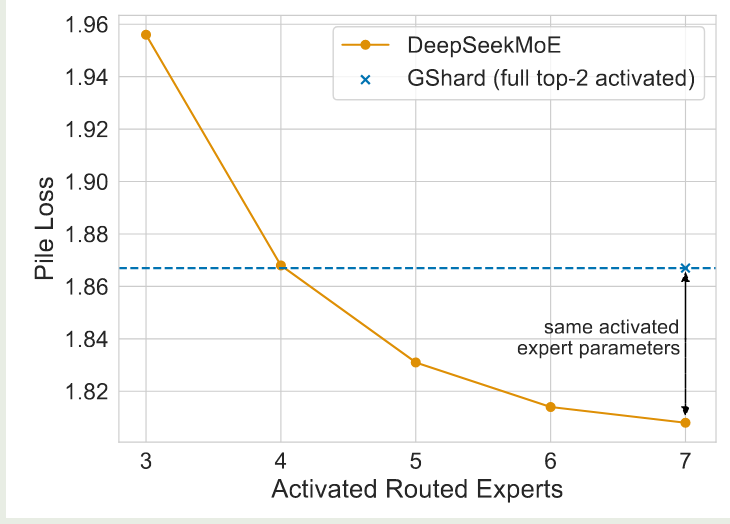
实验结果显示,DeepSeekMoE 仅需激活 4 个路由专家,就可以达到与 GShard 相同的表现。这说明了 DeepSeekMoE 模型中每个专家可以学习到更准确的知识。
Conclusion
作者在本文中提出了 DeepSeekMoE 架构,来提高 MoE 模型中专家的利用效率。为了达到这一点,作者首先使用了更细粒度的专家,降低每个专家的学习成本,然后,作者使用了共享专家,来降低不同专家之间的知识冗余。作者先在 2B 的模型上验证了方法的有效性,然后作者将模型 scale 到了 16B 和 125B。结果显示模型的效果均超过了以前的工作。