Introduction
传统的偏好优化主要基于 RLHF, 其过程为：SFT, reward modeling, RLHF. 其中 reward model 的训练至关重要，对最终模型的表现有非常大的影响。但是 RLHF 的问题在于其训练复杂且经常不稳定。
为了解决这个问题，作者提出了 Direct Preference Optimization (DPO), DPO 通过构建 reward function 和最优策略之间的关系，进而通过训练 policy model 来同时完成 reward model 的训练。这样，我们就避免了 reward model 的训练。结果发现，DPO 的表现超过了之前的偏好优化方法。
Background
作者首先回顾了 RLHF, RLHF 的 pipeline 如下
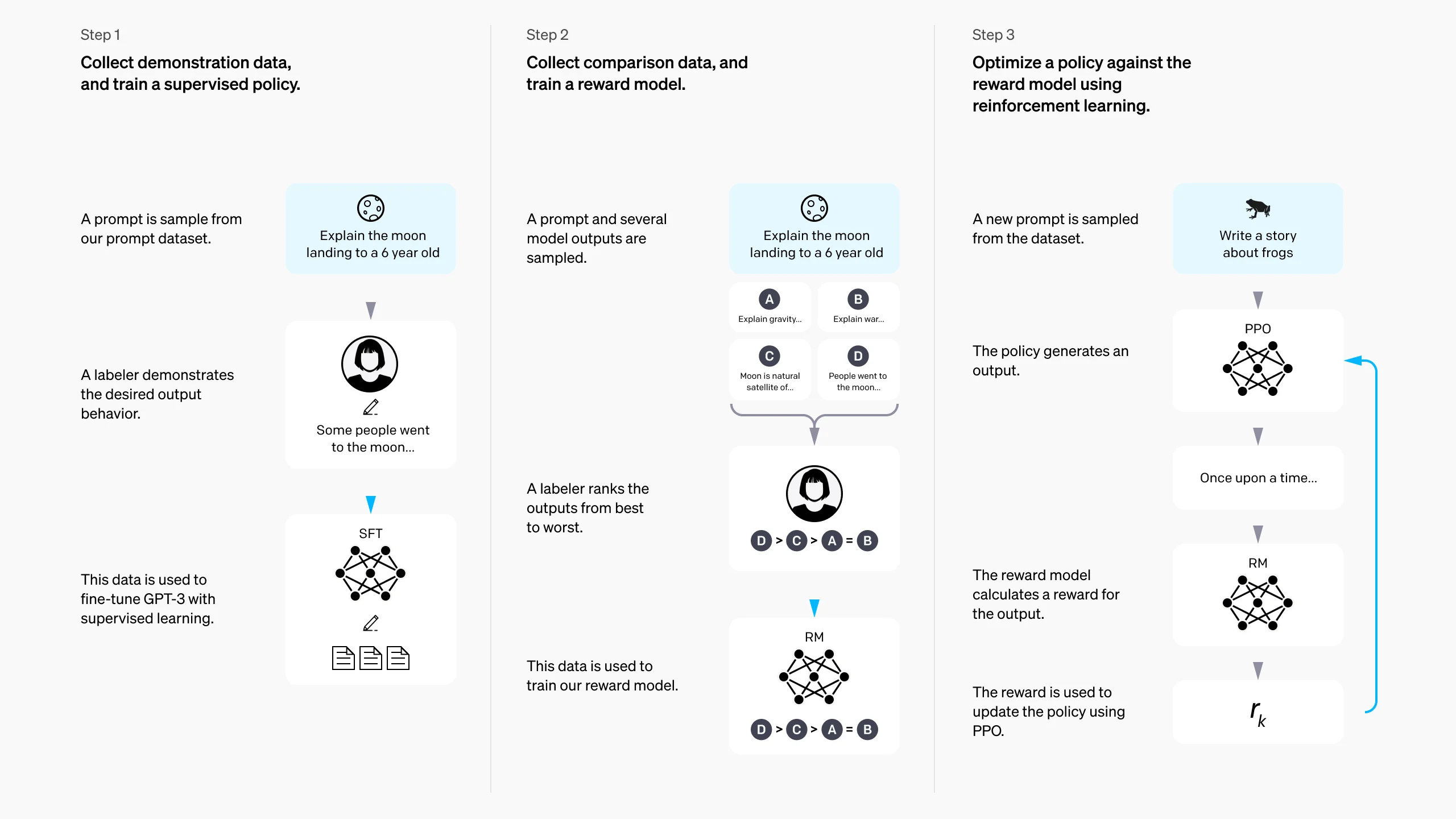
其包含了三个步骤：
SFT RLHF 首先基于 base model 通过 SFT 得到一个初始模型 $\pi^{\mathrm{SFT}}$.
Reward modeling 接下来，我们给定输入 $x$, 对 $\pi^{\mathrm{SFT}}$ 采样得到 $(y_1,y_2)\sim \pi^{\mathrm{SFT}}(y\mid x)$. 输出 $y_1, y_2$ 然后由人类进行打分得到偏好关系 $y_w<y_l\mid x$, 表示 $y_w$ 比 $y_l$ 更符合人类的 pian hao 偏好，一般来说我们假设真实的偏好是由一个 reward function $r^(x,y)$ 产生的，即 $y_w\succ y_l \Leftrightarrow r^(x, y_w)>r^(x, y_l)$. reward modeling 通常基于 Bradley-Terry (BT) 模型得到，BT model 定义人类真实偏好分布 $p^$ 如下：
$$ p^*(y_1>y_2\mid x)= \frac{\exp(r^*(x, y_1))}{\exp(r^*(x, y_1))+\exp(r^*(x, y_2))} $$假设我们从分布 $p^*$ 中采集到一个数据集 $\mathcal{D}={(x^{(i)},y_w^{(i)},y_l^{(i)})}{i=1}^N$, 我们可以通过 MLE 来估计得到一个 reward model $r{\phi}(x,y)$, 通过将这个问题转换为一个二分类问题，我们得到对应的 negative log-likelihood loss 如下：
$$ \mathcal{L}_R(r_\phi, D) = -\mathbb{E}_{(x,y_w,y_l)\sim \mathcal{D}}\left[\log \sigma\left(r_\phi(x,y_w)-r_\phi(x,y_l)\right)\right] $$其中 $\sigma$ 是 logistic function. 在 LLM 中，$r_\phi(x,y)$ 通常由 $\pi^{\mathrm{SFT}}$ 初始化得到，然后我们在 $\pi^{\mathrm{SFT}}$ 最后一层加入一个 linear layer 来得到对应的 reward 的预测值。一般地，为了降低 reward function 的 variance, 之前的工作会进行 normalization, 即 $\mathbb{E}{(x,y)}\sim\mathcal{D}[r{\phi}(x,y)]=0$ for all $x$.
RL fine-tuning 这个阶段，我们基于学习到的 reward function $r_\phi(x,y)$ 来为 LLM 的训练提供奖励，作者使用了和 RLHF 一样的目标函数：
$$ \max_{\pi_\theta}\quad \mathbb{E}_{x\sim \mathcal{D}, y\sim \pi_\theta(y\mid x)}\left[r_\phi(x,y)\right] - \beta\mathbb{D}_{\mathrm{KL}}\left[\pi_\theta(y\mid x)\Vert \pi_{\mathrm{ref}}(y\mid x)\right] $$这里 $\beta>0$ 是超参数，用于控制 $\pi_\theta$ 相对于 $\pi_{\mathrm{ref}}$ 的偏离程度， $\pi_{\mathrm{ref}}$ 一般就是 $\pi^{\mathrm{SFT}}$. 实际上， $\pi_\theta$ 也由 $\pi^{\mathrm{SFT}}$ 初始化.
DPO
DPO 的主要目标是构建一个更简单的 policy optimization 方法。与 RLHF 不同，DPO 跳过了 reward modeling 这一阶段，而是直接使用偏好数据来优化大语言模型
为了实现这个目标，作者第一步就是构建 reward model 和 policy model 之间的关系。注意到
$$ \begin{aligned} &\max_{\pi_\theta}\ \mathbb{E}_{x\sim \mathcal{D}, y\sim \pi_\theta(y\mid x)}\left[r_\phi(x,y)\right] - \beta\mathbb{D}_{\mathrm{KL}}\left[\pi_\theta(y\mid x)\Vert \pi_{\mathrm{ref}}(y\mid x)\right]\\ &= \max_{\pi_\theta}\ \mathbb{E}_{x\sim \mathcal{D}}\mathbb{E}_{y\sim \pi_\theta(y\mid x)}\left[r_\phi(x,y) - \beta\log\frac{\pi_\theta(y\mid x)}{\pi_{\mathrm{ref}}(y\mid x)}\right]\\ &= \min_{\pi_\theta}\ \mathbb{E}_{x\sim \mathcal{D}}\mathbb{E}_{y\sim \pi_\theta(y\mid x)}\left[\log\frac{\pi_\theta(y\mid x)}{\pi_{\mathrm{ref}}(y\mid x)}-\frac{1}{\beta}r_\phi(x,y)\right]\\ &= \min_{\pi_\theta}\ \mathbb{E}_{x\sim \mathcal{D}}\mathbb{E}_{y\sim \pi_\theta(y\mid x)}\left[\log\frac{\pi_\theta(y\mid x)}{\frac{1}{Z(x)}\pi_{\mathrm{ref}}(y\mid x)\exp\left(\frac1\beta r_\phi(x,y)\right)}-\log Z(x)\right]\\ \end{aligned} $$其中 $Z(x)$ 是 partition function, 定义如下
$$ Z(x) = \sum_{y} \pi_{\mathrm{ref}}(y\mid x)\exp\left(\frac1\beta r_\phi(x,y)\right) $$注意到 partition function 只是 $x$ 和 $\pi_{\mathrm{ref}}$ 的函数，而不依赖于 $\pi_\theta$, 因此我们定义
$$ \pi^*(y\mid x) = \frac{1}{Z(x)}\pi_{\mathrm{ref}}(y\mid x)\exp\left(\frac1\beta r_\phi(x,y)\right) $$易知 $\pi^$ 满足 $\pi^(y\mid x)\geq0, \forall y$, 以及 $\sum_y \pi^*(y\mid x)=1$. 因为 $Z(x)$ 不依赖于 $y$, 因此我们可以进一步简化上面的目标函数如下
$$ \begin{aligned} &\min_{\pi_\theta}\ \mathbb{E}_{x\sim \mathcal{D}}\left[\mathbb{E}_{y\sim \pi_\theta(y\mid x)}\left[\log\frac{\pi_\theta(y\mid x)}{\pi^*(y\mid x)}\right]-\log Z(x)\right] \\ &= \min_{\pi_\theta}\ \mathbb{E}_{x\sim \mathcal{D}}\left[\mathbb{D}_{\mathrm{KL}}\left[\pi_\theta(y\mid x)\Vert \pi^*(y\mid x)\right]-\log Z(x)\right]\\ &= \boxed{\min_{\pi_\theta}\ \mathbb{E}_{x\sim \mathcal{D}}\left[\mathbb{D}_{\mathrm{KL}}\left[\pi_\theta(y\mid x)\Vert \pi^*(y\mid x)\right]\right]} \end{aligned} $$而上述目标函数的最小值为 0，当且仅当 $\pi_\theta=\pi^*$, 此时我们的最优 policy 为
$$ \pi_\theta^*(y\mid x) = \pi^*(y\mid x) = \frac{1}{Z(x)}\pi_{\mathrm{ref}}(y\mid x)\exp\left(\frac1\beta r_\phi(x,y)\right),\ \forall x\in\mathcal{D} $$直接求解 $\pi_\theta^$ 非常困难，因为这涉及到 $Z(x)$ 的计算，这个时候作者就提出了一个关键改变，即我们从上述的 $\pi_\theta^$ 反向推到出 $r(x,y)$:
$$ r(x,y) = \beta\log\frac{\pi_\theta(y\mid x)}{\pi_{\mathrm{ref}}(y\mid x)}+\beta\log Z(x) $$我们可以基于这个公式来推到出最优的 reward function $r^$ 以及对应的最优策略 $\pi^$.
此时，我们的表达式里仍然含有 $Z(x)$, 但是当我们使用 Bradley-Terry 模型之后，我们就可以得到真实的人类偏好分布，计算过程如下所示
$$ \begin{aligned} p^*(y_w>y_l\mid x)&= \sigma\left(r_\phi(x,y_w)-r_\phi(x,y_l)\right)\\ &= \boxed{\sigma\left(\beta\log\frac{\pi_\theta(y_w\mid x)}{\pi_{\mathrm{ref}}(y_w\mid x)}-\beta\log\frac{\pi_\theta(y_l\mid x)}{\pi_{\mathrm{ref}}(y_l\mid x)}\right)} \end{aligned} $$这样，基于 MLE 的目标函数就是
$$ \mathcal{L}_{\mathrm{DPO}}(\pi_{\theta};\pi_{\mathrm{ref}})= -\mathbb{E}_{(x,y_w,y_l)\in\mathcal{D}}\left[\sigma\left(\beta\log\frac{\pi_\theta(y_w\mid x)}{\pi_{\mathrm{ref}}(y_w\mid x)}-\beta\log\frac{\pi_\theta(y_l\mid x)}{\pi_{\mathrm{ref}}(y_l\mid x)}\right)\right] $$通过这种方式，我们就避免了 reward model 的训练。
接下来，作者分析了一下 DPO 目标函数的梯度，
$$ \begin{aligned} \nabla_\theta \mathcal{L}_{\mathrm{DPO}}(\pi_{\theta};\pi_{\mathrm{ref}})&=-\nabla_\theta \mathbb{E}_{(x,y_w,y_l)\in\mathcal{D}}\left[\log\sigma(u)\right]\\ &= -\mathbb{E}_{(x,y_w,y_l)\in\mathcal{D}}\left[\frac{\nabla_\theta \sigma(u)}{\sigma(u)}\nabla_\theta u\right]\\ &= -\mathbb{E}_{(x,y_w,y_l)\in\mathcal{D}}\left[\frac{\sigma(u)(1-\sigma(u))}{\sigma(u)}\nabla_\theta u\right]\\ &= -\mathbb{E}_{(x,y_w,y_l)\in\mathcal{D}}\left[(1-\sigma(u))\nabla_\theta u\right]\\ &= -\mathbb{E}_{(x,y_w,y_l)\in\mathcal{D}}\left[\sigma(-u)\nabla_\theta u\right]\\ &= -\mathbb{E}_{(x,y_w,y_l)\in\mathcal{D}}\left[\beta\sigma\left[\beta\log\frac{\pi_\theta(y_l\mid x)}{\pi_{\mathrm{ref}}(y_l\mid x)}-\beta\log\frac{\pi_\theta(y_w\mid x)}{\pi_{\mathrm{ref}}(y_w\mid x)}\right]\left[\nabla_\theta\log\pi(y_w\mid x) - \nabla_\theta \log\pi(y_l\mid x)\right]\right]\\ \end{aligned} $$从梯度来看，当我们的 reward 估计错误时，即 $\sigma(-u)>0$ 时， DPO 会提高 $y_w$ 的生成可能性以及降低 $y_l$ 的生成可能性，从而提高模型对于偏好输出的可能性。
最终，DPO 的 pipeline 如下：
- 收集偏好数据 $y_1,y_2\sim\pi_{\mathrm{ref}}(\cdot\mid x)$, 然后通过人类标注得到偏好数据集 $\mathcal{D}={(x^{(i)},y_w^{(i)},y_l^{(i)})}_{i=1}^N$
- 基于 $\mathcal{L}{\mathrm{DPO}}(\pi{\theta};\pi_{\mathrm{ref}})$ 优化大语言模型参数
一般来说，我们将 $\pi_{\mathrm{ref}}$ 初始化为 $\pi^{\mathrm{SFT}}$, 但是如果我们没有 $\pi^{\mathrm{SFT}}$ 时，我们可以通过最大似然估计来得到 $\pi_{\mathrm{ref}}$, 即
$$ \pi_{\mathrm{ref}} = \arg\max_{\pi}\mathbb{E}_{(x,y_w,y_l)\sim\mathcal{D}}\log \pi(y_w\mid x) $$Theoretical Analysis of DPO
Definition 两个 reward function $r(x,y)$ 和 $r’(x,y)$ 等价当且仅当存在函数 $f$ 满足 $r(x,y)-r’(x,y)=f(x)$。
上述定义给出了一个等价关系，将 reward function 分割成了不同的等价类。接下来，作者给出了两个引理：
第一个引理说明同一个等价类里的 reward function 对应的偏好分布一致
Lemma 1 在 Plack-Luce 框架下，如 Bradley-Terry model, 同一个等价类里的 reward function 得到的偏好分布是一致的
第二个引理说明了最优策略对应的 reward function 都在一个等价类里
Lemma 2 在有限制的情况下，同一个等价类里的 reward function 得到的最优策略是一样的
Lemma 2 说明我们只要从最优的等价类里任意找到一个 reward function, 则最终的效果是一样的。
Theorem 1 假设我们有一个 reference model $\pi_{\mathrm{ref}}(\cdot\mid x)>0$ for all prompt-answer pairs $(x,y)$, 则对于某个模型 $\pi(y\mid x)$, 则与 $\pi_{\mathrm{ref}}$ 对应的等价类里的 reward function 都可以表示为如下形式 $r(x,y) = \beta\frac{\pi(y\mid x)}{\pi_{\mathrm{ref}}(y\mid x)},\ \beta>0$.
我们也可以通过 Theorem 1 来显示推导出 DPO 选择的 reward function:
$$ \sum_{y}\underbrace{\pi_{\mathrm{ref}}(y\mid x)\exp\left(\frac1\beta r_\phi(x,y)\right)}_{\pi(y\mid x)}=1 $$回顾前面 $\pi^*(y\mid x)$ 的定义，我们知道 $\pi(y\mid x)$ 实际上是针对 $r(x,y)$ 推导出来的最优策略的 partition function.
注意到我们的初始目标函数可以改写为如下形式
$$ \min_{\pi_\theta}\ \mathbb{E}_{x\sim \mathcal{D}}\left[\underbrace{r_{\phi}(x,y)-\beta\log Z(x)}_{f(r_\phi, \pi_{\mathrm{ref}},\beta)}-\beta\underbrace{ \frac{\pi_\theta(y\mid x)}{\pi_{\mathrm{ref}}(y\mid x)}}_{\text{KL}}\right] $$此时，我们可以将 $f(r_\phi, \pi_{\mathrm{ref}},\beta)$ 里的 normalization term 视作为 $\pi_{\mathrm{ref}}$ 的 soft value function, 这个 soft value function 不影响最终的结果，但是没有的话会导致训练时的 variance 很高。 DPO 通过 re-parameterization, 得到的奖励函数不需要 baseline, 因而解决了训练不稳定的问题。
Experiments
作者首先对比了不同偏好优化算法的表现，如下图所示
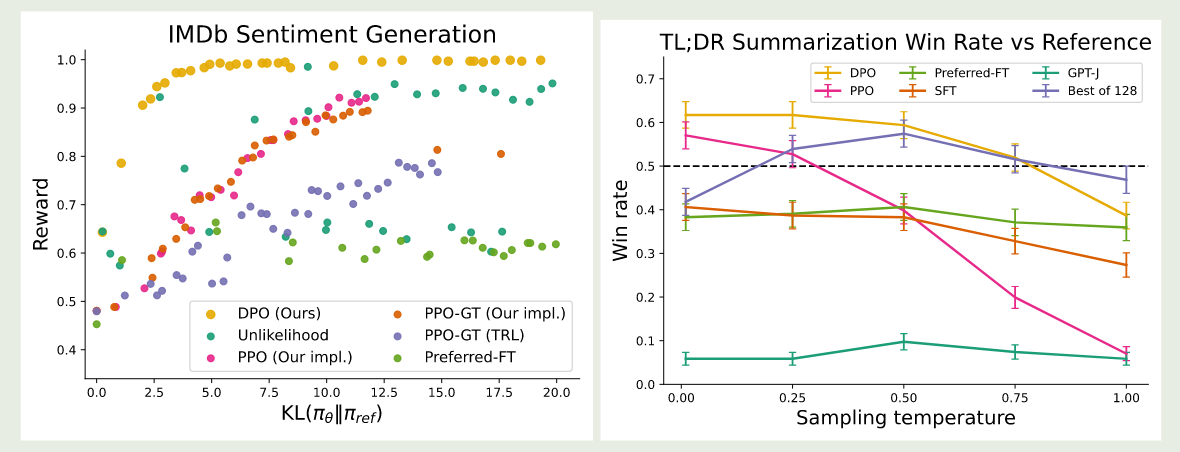
从实验结果可以看到，DPO 对于不同的 KL Values 和不同的采样温度其表现都非常好，并且更加 robust
Conclusion
在本文中，作者提出了 DPO，一个针对 LLM 偏好优化的训练范式，DPO 构建了最优的 policy 与 reward function 之间的关系，从而避免了训练 reward model, 让模型可以直接从偏好数据集中进行学习和训练。