作者提出了 flashattention, 一个通过降低 multi head attention 内存访问开销来提高 attention 计算效率的方法
Introduction
Transformer 的 attention 是一个平方度复杂度的算法,这个平方复杂度既体现在时间复杂度上(矩阵乘法),也体现在空间复杂度上(需要存储中间结果)。因此,要降低 attention 的复杂度,我们有两种思路:
本文提出的 flashattention 就属于降低空间复杂度的一种做法。作者认为,我们应该设计一种 IO-aware 的 attention 算法,来减少 attention 计算式的内存访问开销,进而提高 attention 的计算效率。
作者首先提到,一个未解决的问题就是:
降低 attention 的内存访问开销是否可以提高 attention 的计算效率?
作者发现,已有的一些工作虽然在理论上降低了 attention 的计算效率,但是在实际中,他们的效果并没有提升太多。作者分析原因认为,已有工作主要关注于降低 FLOPs, 但是忽略了内存访问开销。
因此,作者在本文中就提出了 flashattention, 一个 IO-aware 的 attention 算法,作者通过尽可能降低内存访问开销来提高模型的计算效率。具体做法就是,避免从内存中读写 attention matrix, 作者认为这个目标有两个挑战:
- 计算 softmax 的时候不访问所有的输入
- 在反向传播时不存储中间的 attention matrix
作者提出了两个方法来分别解决这两个问题:
- 作者使用了 tiling 技巧,将 input 分成多个 block, 然后分别进行处理,进而降低 softmax 的内存访问开销
- 作者使用了 recompute 技巧,在反向传播时,重新计算 softmax normalization factor
通过这些改进,我们可以让 attention 运行更快,并且降低内存访问开销。
作者还从理论上分析了 flashattention 的复杂度,提供了理论基础。
作者通过实验验证了 flashattention 的有效性,主要是三点:
- 训练效率更高:相比于 Huggingface 和 Megatron, flashattention 的训练效率提升了 2-3 倍
- 模型的表现更好:相比于 GPT-2, 模型的 perplexity 提升了 0.7 个点左右
- 速度更快:flashattention 比标准的 attention 实现快 3 倍以上
Background
Hardware Performance
作者首先介绍了以下 GPU 的内存架构,如下图所示
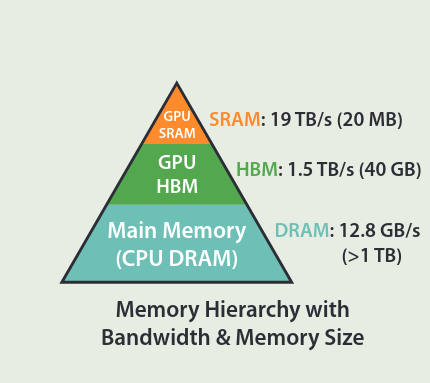
可以看到,GPU 内存可以分为三个层级:
- SRAM: GPU 的寄存器,容量小,但是访问速度极快
- High bandwith memory (HBM): GPU 的高速内存,访问速度较快,容量中等
- DRAM: CPU 内存,容量最大,但是访问速度较慢
接下来作者介绍了 Execution model 的概念,GPU 有多个线程来执行同一个操作(SPMD),这个操作也被称为 kernel, kernel 会从 HBM 中加载输入到 SRAM 中进行计算,然后写回 HBM.
对一个算法,我们可以将其归类为 compute-bound 和 memory-bound 两类, 我们可以用 arithmetic intensity 来进行区分,arithmetic intensity 定义为 arithmetic operations 与 memory access 的比率。
- compute bound: 算法的瓶颈在于算力,由于算力不足导致运行时间慢,比如矩阵乘法
- memory-bound: 算法的瓶颈在于内存访问效率,比如 element-wise 操作或者是 reduction
为了提高 memory-bound 类型算法的效率,我们进行 kernel fusion, 即把多个访问同一片内存的操作放在一起处理,避免多次读写内存
Standard Attention Implementation
作者还回顾了一下标准化的 attention 实现。
Forward Pass
给定 $Q,K,V\in\mathbb{R}^{N\times d}$, 其中 $N$ 是序列长度, $d$ 是 head dimension, attention 的定义如下
$$ S = QK^T\in\mathbb{R}^{N\times N},\quad P = \mathrm{softmax}(S)\in\mathbb{R}^{N\times N},\quad O = PV\in\mathbb{R}^{N\times d} $$这里 $\mathrm{softmax}$ 是逐行计算的。
算法的执行过程如下

我们有第一个结论
Proposition 1 标准化 attention 前向传播时访问 HBM 的内存访问开销为 $\mathcal{O}(Nd+N^2)$.
证明:对于 attention, 我们需要从 HBM 中加载 $Q,K,V\in\mathbb{R}^{N\times d}$, 然后输出 $O\in\mathbb{R}^{N\times d}$ 并保存到内存中。
首先我们需要计算 $S = QK^T$, 这一步需要加载 $Q,K$ 并将 $S$ 保存到 HBM 中,内存访问量为 $\mathcal{O}(Nd+N^2)$.
接下来,我们需要计算 $P = \mathrm{softmax}(S)$, 这一步需要加载 $S$ 然后将 $P$ 保存到 HBM 中,内存访问量为 $\mathcal{O}(N^2)$.
最后,我们需要计算 $O = PV$, 这一步需要加载 $P$ 和 $V$ 然后将 $O$ 保存到 HBM 中,内存访问量为 $\mathcal{O}(Nd+N^2)$.
总的来说,标准化 attention 的内存访问开销为 $\mathcal{O}(Nd+N^2)$.
Backward Pass
标准 attention 反向传播过程如下图所示

Proposition 2 标准化 attention 反向传播时访问 HBM 的内存访问开销为 $\mathcal{O}(Nd+N^2)$.
证明:对于标准化 attention 的反向传播,我们需要从 HBM 中加载 $Q,K,V,dO\in\mathbb{R}^{N\times d}$ , 然后输出 $dQ,dK,dV$ 并保存到 HBM 中。
首先我们计算 $dV=P^TdO$, 这一步需要加载 $P,dO$ 并将 $dV$ 保存到 HBM 中,内存访问开销为 $\mathcal{O}(Nd+N^2)$.
接下来我们计算 $dP=dOV^T$, 这一步需要加载 $dO, V$ 并将 $dP$ 保存到 HBM 中,内存访问开销为 $\mathcal{O}(Nd)$.
然后我们计算 $dS$, 这一步需要加载 $P$ 并将 $dS$ 保存到 HBM 中,内存访问开销为 $\mathcal{O}(N^2)$.
对于 $dQ$ 和 $dK$ 的计算,内存访问开销都是 $\mathcal{O}(Nd+N^2)$.
因此,标准化 attention 的内存访问开销为 $\mathcal{O}(Nd+N^2)$.
Method
作者在本节首先介绍了 flashattention 算法,然后作者证明了 flashattention 的正确性以及分析了复杂度。最后作者对 flashattention 进行扩展得到了 Block-sparse Flashattention.
Flashattention
attention 模块的输入是 $Q,K,V\in\mathbb{R}^{N\times d}$, 输出是 $O\in\mathbb{R}^{N\times d}$, 作者的目标是减少计算过程中的 HBM 访问次数
作者分别使用了 tiling 和 recomputation 来解决 attention 前向传播和反向传播中的内存访问开销。flashattention 的核心思想是,我们将 $Q,K,V$ 分割成 block, 然后在 block 层面进行加载和计算。
Tiling
首先作者介绍了一下如何使用 tiling 来计算 softmax.
给定一个向量 $x\in\mathbb{R}^{B}$, 其 softmax 计算方式如下
$$ m(x) = \max_i x_i,\ f(x) = [e^{x_1-m(x)},\dots,e^{x_B-m(x)}], \ \ell(x)=\sum_if(x)_i, \ \mathrm{softmax}(x) = \frac{f(x)}{\ell(x)} $$如果我们现在有两个向量 $x^{(1)}, x^{(2)}\in\mathbb{R}^{B}$, 记 $x=[x^{(1)}, x^{(2)}]^T\in\mathbb{R}^{2B}$, 我们可以将 $\mathrm{softmax}(x)$ 的计算分解为
$$ \begin{aligned} m(x) &= \max(m(x^{(1)}), m(x^{(2)})), f(x) = [e^{m(x^{(1)})-m(x)}f(x^{(1)}),e^{m(x^{(2)})-m(x)}f(x^{(2)})]\\ \ell(x) &= e^{m(x^{(1)})-m(x)}\ell(x^{(1)}) + e^{m(x^{(2)})-m(x)}\ell(x^{(2)}), \mathrm{softmax}(x) = \frac{f(x)}{\ell(x)} \end{aligned} $$因此,如果我们额外记录 $m(x)$ 以及 $\ell(x)$ 这两个量,那么我们可以每次仅计算 softmax 的一个 block. 具体细节见softmax.
Recomputation
在反向传播过程中,一般我们需要存储 $S,P\in\mathbb{R}^{N\times N}$, 需要的空间复杂度为 $\mathcal{O}(N^2)$. 但是,通过存储 $O\in\mathbb{R}^{N\times d}$ 以及 $(m,\ell)$, 我们可以避免重新计算 $S,P$,这可以看做是 gradient checkpointing. 但是与 checkpointing 相比,因为 flashattention 减少了内存访问开销,因此其反向过程并没有变得更慢。
Algorithm
最终,flashattention 的算法如下图所示

Analysis
Correctness
算法的正确性由定理 1 给出
Theorem 1 flashattention (即算法 1) 输出 $O=\mathrm{softmax}(QK^T)V$, 其时间复杂度为 $\mathcal{O}(N^2d)$, 空间复杂度为 $\mathcal{O}(N)$.
证明:时间复杂度主要由矩阵乘法决定。在计算 $S_{ij}=Q_iK_j^T$ 时,所花费的 FLOPS 为 $\mathcal{O}(B_rB_cd)$. 在计算 $\tilde{P}_{ij}V_j$ 时,所花费的 FLOPS 为 $\mathcal{O}(B_rB_cd)$. 循环一共执行了
$$ T_cT_r = \left\lceil\frac{N}{B_c}\right\rceil\left\lceil\frac{N}{B_r}\right\rceil $$从而总的 FLOPS 为
$$ \mathcal{O}\left(\frac{N^2}{B_rB_c}B_rB_cd\right) = \mathcal{O}(N^2d) $$在 flashattention 的计算过程中,我们只需要保存 $(\ell, m)$ 即可,因此需要的额外内存空间为 $\mathcal{O}(N)$.
接下来,我们可以证明 flashattention 的正确性,我们使用归纳法来证明。令 $j$ 满足 $0\leq j\leq T_c$, $K_{:j}\in\mathbb{R}^{jB_c\times d}$, $V_{:j}\in\mathbb{R}^{jB_c\times d}$ 分别为 $K$ 和 $V$ 的前 $jB_c$ 行。 $S_{:, :j}=QK_{:j}^T\in\mathbb{R}^{N\times jB_c}$, $P_{:,:j}=\mathrm{softmax}(S_{:,:j})\in\mathbb{R}^{N\times jB_c}$, $m^{(j)}, \ell^{(j)}, O^{(j)}$ 分别为 $m,\ell, O$ 的第 $j$ 个元素。我们证明经过第 $j$ 次迭代后,HBM 中保存的是
$$ m^{(j)}=\mathrm{rowmax}(S_{:,:j})\in\mathbb{R}^N, \ell^{(j)}=\mathrm{rowsum}(\exp(S_{:,:j}-m^{(j)}))\in\mathbb{R}^N, O^{(j)} = P_{:,:j}V_{:j}\in\mathbb{R}^{N\times d} $$当 $j=0$ 时,上面的结果显然成立。现在我们假设对某个 $j=0,\dots, T_c-1$ 上面的结果成立,我们需要证明对 $j+1$ 也成立。
首先
$$ m^{(j+1)}=\max(m^{(j)}, \tilde{m}) = \max(\mathrm{rowmax}(S_{:,:j}), \mathrm{rowmax}(S_{:,j:j+1}))=\mathrm{rowmax}(S_{:,:j+1}) $$接下来
$$ \begin{aligned} \ell^{(j+1)} &= \exp(m^{(j)}-m^{(j+1)})\ell^{(j)} + \exp(\tilde{m}-m^{(j+1)})\tilde{\ell}\\ &=\exp(m^{(j)}-m^{(j+1)})\mathrm{rowsum}(\exp(S_{:,:j}-m^{(j)})) + \exp(\tilde{m}-m^{(j+1)})\mathrm{rowsum}(\exp(S_{:,j:j+1}-\tilde{m}))\\ &= \mathrm{rowsum}(\exp(S_{:,:j}-m^{(j+1)})) + \mathrm{rowsum}(\exp(S_{:,j:j+1}-m^{(j+1)}))\\ &= \mathrm{rowsum}(\exp(S_{:,:j+1}-m^{(j+1)})) \end{aligned} $$最后,我们计算 $O^{(j+1)}$ 得到:
$$ \begin{aligned} O^{(j+1)} &= \mathrm{diag}(\ell^{(j+1)})^{-1}(\mathrm{diag}(\ell^{(j)})\exp(m^{(j)}-m^{(j+1)})O^{(j)}+\exp(\tilde{m}-m^{(j+1)})\exp(S_{:,j:j+1}-\tilde{m})V_{:,j:j+1})\\ &= \mathrm{diag}(\ell^{(j+1)})^{-1}(\mathrm{diag}(\ell^{(j)})\exp(m^{(j)}-m^{(j+1)})P_{:,:j}V_{:,:j}+\exp(-m^{(j+1)})\exp(S_{:,j:j+1})V_{:,j:j+1})\\ &= \mathrm{diag}(\ell^{(j+1)})^{-1}(\mathrm{diag}(\ell^{(j)})\exp(m^{(j)}-m^{(j+1)})\mathrm{diag}(\ell^{(j)})^{-1}\exp(S_{:,:j}-m^{(j)})V_{:,:j}+\exp(-m^{(j+1)})\exp(S_{:,j:j+1})V_{:,j:j+1})\\ &= \mathrm{diag}(\ell^{(j+1)})^{-1}(\exp(-m^{(j+1)})\exp(S_{:,:j}))V_{:,:j}+\exp(-m^{(j+1)})\exp(S_{:,j:j+1})V_{:,j:j+1})\\ &= \mathrm{diag}(\ell^{(j+1)})^{-1}( \begin{bmatrix} \exp(S_{:,:j}-m^{(j+1)}) & \exp(S_{:,:j}-m^{(j+1)}) \end{bmatrix}\begin{bmatrix} V_{:,:j} \\ V_{:,j:j+1} \end{bmatrix}\\ &= \mathrm{softmax}(S_{:,:j+1})V_{:,:j+1} \end{aligned} $$因此上面的结果对 $j+1$ 也成立,从而 flashattention 的结果对 $j=0,\dots,T_c$ 都成立。
Forward Pass of flashattention
第一个问题是如何提高 softmax 计算的效率,作者的做法先先计算 normalization constant 然后再分别计算不同的 column.
给定 $Q,K,V\in\mathbb{R}^{N\times d}$, 其中 $N$ 是序列长度, $d$ 是 head dimension, attention 的定义如下
$$ S = QK^T\in\mathbb{R}^{N\times N},\quad P = \mathrm{softmax}(S)\in\mathbb{R}^{N\times N},\quad O = PV\in\mathbb{R}^{N\times d} $$我们有 $S_{ij}=q_i^Tk_j$, 这里 $q_i$ 和 $k_j$ 分别是 $Q$ 和 $K$ 的第 $i$ 列以及第 $j$ 列, normalization constant 定义为:
$$ L_i = \sum_{j=1}^N \exp\left(q_i^Tk_j\right) $$对任意 $i$, 计算 $L_i$ 只需要 $\mathcal{O}(N)$ 的空间复杂度。
令 $v_j$ 是 $V$ 的第 $i$ 列,则输出 $O$ 的第 $i$ 列 $o_i$ 为
$$ o_i = P_{i:}V = \sum_{j=1}^N P_{ij}v_j = \sum_{j=1}^N\frac{\exp(q_i^Tk_j)}{L_i}v_j $$这个过程中,对任意 $i$, 计算 $o_i$ 也只需要 $\mathcal{O}(N)$ 的空间复杂度。
因此,在 $L_i$ 已经计算好的情况下,我们可以在 $\mathcal{O}(N)$ 的空间复杂度下计算 $o_i$.
最终,flashattention 的 forward pass 过程如下图所示

接下来,作者分析了 flashattention 的内存访问开销。结论如下
Theorem 2 令 $N$ 为 sequence length, $d$ 为 head dimension, $M$ 是 SRAM 的 size, 且满足 $d\leq M\leq Nd$. 则 flashattention 前向传播的内存访问开销为 $\Theta(N^2d^2M^{-1})$.
证明:由 Algorithm 1(或者 Algorithm 2)可以知道,$K$ 和 $V$ 的每一个元素都只需要从 HBM 中加载一次,而每一次外层循环都会从 HBM 中加载一次 $O$ 和 $Q$, 因此总的 HBM 访问次数为 $\mathcal{O}(Nd+NdT_c)=\mathcal{O}(NdT_c)$.
接下来,我们给出每一次内层循环的内存访问开销,这是由 SRAM 的大小决定的。由于我们需要 SRAM 可以存储 $K_j\in\mathbb{R}^{B_c\times d}$ 以及 $V_j\in\mathbb{R}^{B_c\times d}$ ,我们的 block size 需要满足
$$ B_cd = \mathcal{O}(M) \Rightarrow B_c = \mathcal{O}\left(\frac{M}{d}\right) $$同理,对于 $O$ 和 $Q$, 我们有
$$ B_rd = \mathcal{O}(M) \Rightarrow B_r = \mathcal{O}\left(\frac{M}{d}\right) $$最后,我们还需要 SRAM 可以存储 $S_{ij}\in\mathbb{R}^{B_r\times B_c}$, 因此
$$ B_rB_c=\mathcal{O}(M) $$这样,
$$ B_c = \mathcal{O}\left(\frac{M}{d}\right), B_r=\mathcal{O}\left(\min\left(\frac{M}{d},\frac{M}{B_c}\right)\right)=\mathcal{O}\left(\min\left(\frac{M}{d},d\right)\right) $$从而
$$ T_c = \frac{N}{B_c} = \mathcal{O}\left(\frac{Nd}{M}\right) $$最终,总的内存访问开销为
$$ \mathcal{O}(NdT_c) = \mathcal{O}\left(\frac{N^2d^2}{M}\right) $$一般来说, $d$ 的大小为 $64-128$, $M$ 的大小为 $100 KB$ 左右, $d^2« M, 因此 flashattention 的内存访问开销远小于标准化 attention 的内存访问开销。
作者还证明 flashattention 的内存访问开销是一个下界,即
Proposition 3 令 $N$ 为 sequence length, $d$ 为 head dimension, $M$ 是 SRAM 的 size, 且满足 $d\leq M\leq Nd$. 则不存在一个对任意 $M\in[d,Nd]$ 都可以在 内存访问开销为 $\Theta(N^2d^2M^{-1})$ 的条件下完成 attention 计算的算法。
证明可以用反证法,基本思想是加载 $Q,K,V$ 的 HBM 访问次数至少为 $\mathcal{O}(Nd)$.
Backward Pass of flashattention
第二个问题是能否在线性空间复杂度下计算 attention 的反向传播过程。
首先我们记损失函数为 $\phi$, 然后令 $\phi$ 对 $O,Q,K,V$ 的梯度分别为 $dO,dQ,dK, dV\in\mathbb{R}^{N\times d}$, 我们的目标是计算 $dQ, dK, dV$.
$dV$ 的计算是最容易的,我们有 $dV=P^TdO$, 因此
$$ dv_j = \sum_{i=1}^N P_{ij}do_i = \sum_{i=1}^N\frac{\exp(q_i^Tk_j)}{L_i}do_i $$由于我们已经计算了 $L_i$, 因此,$dv_j$ 只需要 $\mathcal{O}(d)$ 的空间复杂度。
接下来,注意到 $dP=dOV^T$, 因此我们有
$$ dP_{ij} = do_i^Tv_j $$计算的空间复杂度也是要 $\mathcal{O}(N)$ 的
注意到 $P_{i:}=\mathrm{softmax}(s_{i:})$, 且 $y=\mathrm{softmax}(x)$ 的 Jacobian 是 $\mathrm{diag}(y)-yy^T$ (推导过程见 softmax), 我们有
$$ dS_{i:} = (\mathrm{diag}(P_{i:})-P_{i:}P_{i:}^T)dP_{i:} = P_{i:} \odot dP_{i:} - (P_{i:}^TdP_{i:})P_{i:} $$我们定义
$$ D_i = P_{i:}^TdP_{i:}= \sum_{j=1}^N\frac{\exp(q_i^Tk_j)}{L_i}do_i^Tv_j = do_i^T\sum_{j=1}^N\frac{\exp(q_i^Tk_j)}{L_i}v_j = do_i^To_i $$$D_i$ 的空间复杂度也只需要 $\mathcal{O}(N)$.
则
$$ dS_{i:} =P_{i:} \odot dP_{i:} - D_iP_{i:} $$我们有
$$ dS_{ij} = P_{ij}dP_{ij} - D_iP_{ij} = P_{ij}(dP_{ij}-D_i) $$注意到 $S_{ij}=q_i^Tk_j$, 我们有
$$ dq_i = \sum_{j=1}^N dS_{ij}k_j = \sum_{j=1}^NP_{ij}(dP_{ij}-D_i)k_j = \sum_{j=1}^N\frac{\exp(q_i^Tk_j)}{L_i}(do_i^Tv_j-D_i)k_j $$因此计算 $dq_i$ 的空间复杂度为 $\mathcal{O}(d)$.
同样的,
$$ dk_j = \sum_{j=1}^N dS_{ij}q_i = \sum_{j=1}^NP_{ij}(dP_{ij}-D_i)q_i = \sum_{j=1}^N\frac{\exp(q_i^Tk_j)}{L_i}(do_i^Tv_j-D_i)q_i $$其空间复杂度为 $\mathcal{O}(N)$.
总之,attention 的反向传播过程所需要的空间复杂度为 $\mathcal{O}(N)$.
作者发现有两点可以改进:
- attention mask 不需要存储,我们只需要保存 forward pass 时的输入,然后在 backward pass 时重新生成即可,这样只需要 $\mathcal{O}(N)$ 的空间复杂度。
- 计算 softmax 的梯度是,如果使用公式 $D_i=P_{i:}^TdP_{i:}$ 来计算的话,由于 $P_{i:}\in\mathbb{R}^N$, 可能会导致超过 SRAM 的内存使用限制,因此,我们可以使用 $D_i=do_i^To_i$ 来避免这个问题,其中 $o_i\in\mathbb{R}^d$.
最终,flashattention 的 backward pass 过程如下图所示

经过前面的分析,flashattention 的反向传播的时间复杂度为 $\mathcal{O}(N^2)$, 空间复杂度为 $\mathcal{O}(N)$.
Theorem 5 令 $N$ 为 sequence length, $d$ 为 head dimension, $M$ 是 SRAM 的 size, 且满足 $d\leq M\leq Nd$. 则 flashattention 反向传播的内存访问开销为 $\Theta(N^2d^2M^{-1})$.
定理的证明与 Theorem 2 基本一致,我们此处不再赘述。
Block-sparse Flashattention
当 attention 具有 block sparsity 的性质时,作者提出了 blck-sparse flashattention 来进一步提高 attention 的计算效率。
给定 $Q,K,V\in\mathbb{R}^{N\times d}$, 以及一个 mask $M\in\{0,1\}^{N\times N}$, 我们需要计算
$$ S = QK^T\in\mathbb{R}^{N\times N},\quad P = \mathrm{softmax}(S\odot \mathbb{1}_{M})\in\mathbb{R}^{N\times N},\quad O = PV\in\mathbb{R}^{N\times d} $$其中当 $M_{kl}=1$ 时, $(S\odot \mathbb{1}_ {M})_ {kl}=S_ {kl}$, 否则 $(S\odot \mathbb{1}_ {M})_{kl}=0$.
Block-sparse attention 的算法如下所示

Proposition 4 令 $N$ 为 sequence length, $d$ 为 head dimension, $M$ 是 SRAM 的 size, 且满足 $d\leq M\leq Nd$. 则 block-sparse attention 的内存访问开销为 $\Theta(Nd+N^2d^2M^{-1}s)$, 其中 $s$ 是 block-sparse mask 中的非零 block 的比例
证明与 Theorem 2 的证明是类似的,总的内存访问开销为 $\mathcal{O}(Nd+NdT_c)$, 但是在计算的过程中,由于 mask 矩阵的 block-sparsity, 我们实际上只需要计算一小部分 $M_{ij}\neq0$ 的情况,因此最终的内存访问开销为
$$ \mathcal{O}\left(Nd+\frac{N^2d^2}{M}s\right) $$可以看到,attention mask 的 sparsity 越高,block-sparse flashattention 的效率也就越高。当 $N$ 非常大时,$s 通常为 $1/\sqrt{N}$ 或者 $N^{-1}\log N$, 从而最终的内存访问开销为 $\mathcal{O}(N\sqrt{N})$ 或者 $\mathcal{O}(N\log N)$.
作者对比了以下 block-sparse flashattention 和 flashattention 的效率对比,结果如下图所示
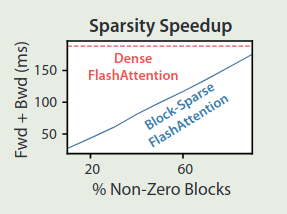
Experiment
作者通过实验验证了 flashattention 的有效性,如下表所示
| Attention | Standard | FlashAttention |
|---|---|---|
| GFLOPs | 66.6 | 75.2 |
| HBM R/W (GB) | 40.3 | 4.4 |
| Runtime (ms) | 41.7 | 7.3 |
可以看到,尽管 flashattention 相比于标准化 attention 需要更多的算力,但是由于其内存访问开销更少,所以最终的运行时间大有了大幅度降低
作者还探究了 block size 对 flashattention 性能对的影响,实验结果如下图所示
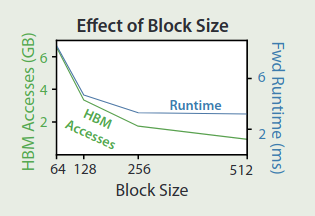
可以看到,随着 block size 增加,循环次数降低,内存访问开销也逐渐降低。但是当 block size 充分大 ( $> 256$) 之后,运行时间就会被别的因素所限制,并且过大的 block size 可能会导致 SRAM 的内存溢出
作者首先在 BERT 和 GPT-2 上验证了 flashattention 的表现,BERT 的实验结果如下表所示
| BERT Implementation | Training time (minutes) |
|---|---|
| Nvidia MLPerf 1.1 | $20.0\pm1.5$ |
| FlashAttention (ours) | $17.4\pm1.4$ |
GPT-2 的实验结果如下表所示
| Model implementations | OpenWebText (ppl) | Training time (speedup) |
|---|---|---|
| GPT-2 small - Huggingface | 18.2 | 9.5 days (1.0 ) |
| GPT-2 small - Megatron-LM | 18.2 | 4.7 days (2.0 ) |
| GPT-2 small - FlashAttention | 18.2 | 2.7 days (3.5 ) |
| GPT-2 medium - Huggingface | 14.2 | 21.0 days (1.0 ) |
| GPT-2 medium - Megatron-LM | 14.3 | 11.5 days (1.8 ) |
| GPT-2 medium - FlashAttention | 14.3 | 6.9 days (3.0 ) |
实验结果显示,flashattention 比 Huggingface 快 3 倍左右,比 Megatron 快 1.7 倍左右
- 训练速度:实验显示,flashattention 在 BERT 上,比 MLPerf 1.1 快 $15\%$, 在 GPT-2 上比 HuggingFace 快 3 倍,比 Megatron 快 1.8 倍
- 准确率:flashattention 是第一个在 Path-X 上比随机表现更好的 transformer 模型;block-sparse flashattention 是第一个在 Path-256 上比随机表现更好的的 sequence model
Conclusion
作者提出了 flashattention, 一个通过优化标准 attention 内存访问效率来提高 attention 计算效率的方法,作者详细介绍了算法设计的原理与证明,并通过实验证明了结果的有效性。