Introduction
现有的大部分模型都基于 Transformer 提出的 softmax attention (SDPA), 虽然也有相关的改进工作,但是主要集中于降低 attention 计算复杂度,提高 attention 在推理时的内存使用效率等。之前的工作提出了关于 attention 的两个问题:
- attention sink, 即模型的注意力会放在初始几个 token 上, 这限制了模型的上下文扩展能力
- massive activation, 少部分 token 的 hidden states 会非常大,这限制了模型的训练稳定性
在本文中,作者通过在 attention 中加入 gating 机制来探索 gating 对模型表现和训练稳定性的影响。尽管 gating 并没有降低 attention 计算复杂度,但是 gating 提出了一个新的视角,即 sparity 与 attention sink 和 massive activation 息息相关,这为后面 sparse attention 的研究提供了 Insight.
作者发现,对 Multi head attention 的输出进行 head-specific gating 的效果最好,并且这种方式还可以提高训练稳定性,模型的表达能力和长上下文能力。作者还进一步分析了这种 gating 方式更好的原因,发现有两点:
- non-linearity: 通过 gating 可以有效提高 output projection layer 输入的秩,进而提高表达能力
- sparsity: gating 可以降低 massive activation 和 attention sink 的影响
作者最终推荐使用 element-wise SDPA gating 方式来进行训练
Related Work
作者主要介绍了 gating 和 attention sink 这两部分的工作。
gating 早在 LSTM 和 GRU 使其就得到了广泛的运用,在 transformer 之后,相关的现行注意力也有应用,比如 MiniMax-01 所使用的 Lightning Attention 等,但是这些工作没有系统性探究 gating 背后的机制。
第二部分是 attention sink, attention sink 现象由 StreamingLLM 提出, 即模型会将相当一部分注意力权重方开始开始的几个 token 上。而本文提出的 gating 机制可以缓解 attention sink 现象。
Method
首先是标准 MHA 定义:
$$ \begin{aligned} Q &= XW_Q, K=XW_K, V=XW_V\\ \mathrm{Attn}_i(Q,K,V) &= \mathrm{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V, i=1,\dots,h\\ \mathrm{MHA}(Q, K, V) &= \mathrm{Concat}([\mathrm{Attn}_1,\dots,\mathrm{Attn}_h])\\ O &= \mathrm{MHA}(Q, K, V) W_O \end{aligned} $$这里 $X\in\mathbb{R}^{n\times d}$ 是 transformer layer pre-normalization 的输出(或者 attention block 的输入), $n$ 是 sequence length, $d$ 是 hidden size, $h$ 是 number of heads, $d_k$ 是 head dimension.
接下来,作者介绍了不同的 gating 策略。这里作者用同一的公式来进行表示
$$ Y' = g(Y,X,W_\theta, \sigma) = Y\odot \sigma(XW_\theta) $$这里 $Y$ 是输入, $X$ 是 attention 的输入,$W_\theta$ 是可学习权重
Position 首先是位置,作者考虑了如下几种变体:
$$ \begin{align} \mathrm{MHA}(Q, K, V)' &= \mathrm{MHA}(Q, K, V)\odot \sigma\left(X W_\theta)\right) \tag{G1}\\ Q' &= Q\odot \sigma\left(XW_\theta\right) \tag{G2}\\ K' &= K\odot \sigma\left(XW_\theta\right) \tag{G3}\\ V' &= V\odot \sigma\left(XW_\theta\right) \tag{G4}\\ O' &= O\odot \sigma\left(XW_\theta\right) \tag{G5}\\ \end{align} $$这里 $\sigma$ 是激活函数,$W_\theta$ 是激活函数的可学习参数,我们可以将其理解为一个 linear layer, 即当前模块的输出取决于输入 hidden sates 经过一个线性层和激活层之后的结果,相似的做法还有 MoE 中的 gating layer, NSA 中的 gating layer 等。对应的示意图如下所示
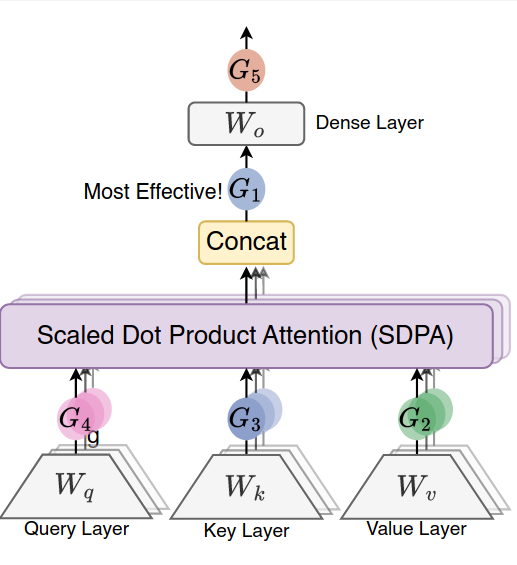
granularity 作者设计了不同粒度的 gating(假设输入为 $X\in\mathbb{R}^{n\times h\times d_k}$):
- head-shared: 不同 head 共享 gating score,
Y'[i,h,k]=gate[i,k]*Y[i,h,k] - head-wise: 同一个 head 共享 gating score,
Y'[i,h,:]=gate[i,h]*Y[i,h,:] - element-wise: 不同元素不共享 gating score,
Y'[i,h,k]=gate[i,h,k]*Y[i,h,k]
从 attention 的角度看,不同 head 本身就承担不同的语义子空间,如果强行共享 gating,会破坏这种分工。
format 作者还构建了 multiplication 和 addition 两种形式:
- multiplication: $Y'=Y\odot \sigma(XW_\theta)$
- addition: $Y'=Y+\sigma(XW_\theta)$
activation function 本文中作者使用了 SiLU 和 sigmoid 两种形式,即
$$ \sigma_{\mathrm{sigmoid}}(x) = \frac{1}{1+e^{-x}},\quad \sigma_{\mathrm{SiLU}} = x*\sigma_{\mathrm{sigmoid}}(x)=\frac{x}{1+e^{-x}} $$Experiments
作者构建了三个模型进行实验,模型配置如下表所示
| Model | 1.7B-28 layers | 1.7B-48 layers | 15B-A2.4B MoE |
|---|---|---|---|
| Layers | 28 | 48 | 24 |
| query heads | 16 | 16 | 32 |
| key/value heads | 8 | 8 | 4 |
| head dim | 128 | 128 | 128 |
| tie embedding | yes | yes | no |
| QK normalization | yes | yes | yes |
| hidden size | 2048 | 1536 | 2048 |
| ffn hidden size | 6144 | 4608 | 768 |
| experts | - | - | 128 |
| top-K | - | - | 8 |
首先是不同 gating 方法对 MoE model 影响,结果如下图所示
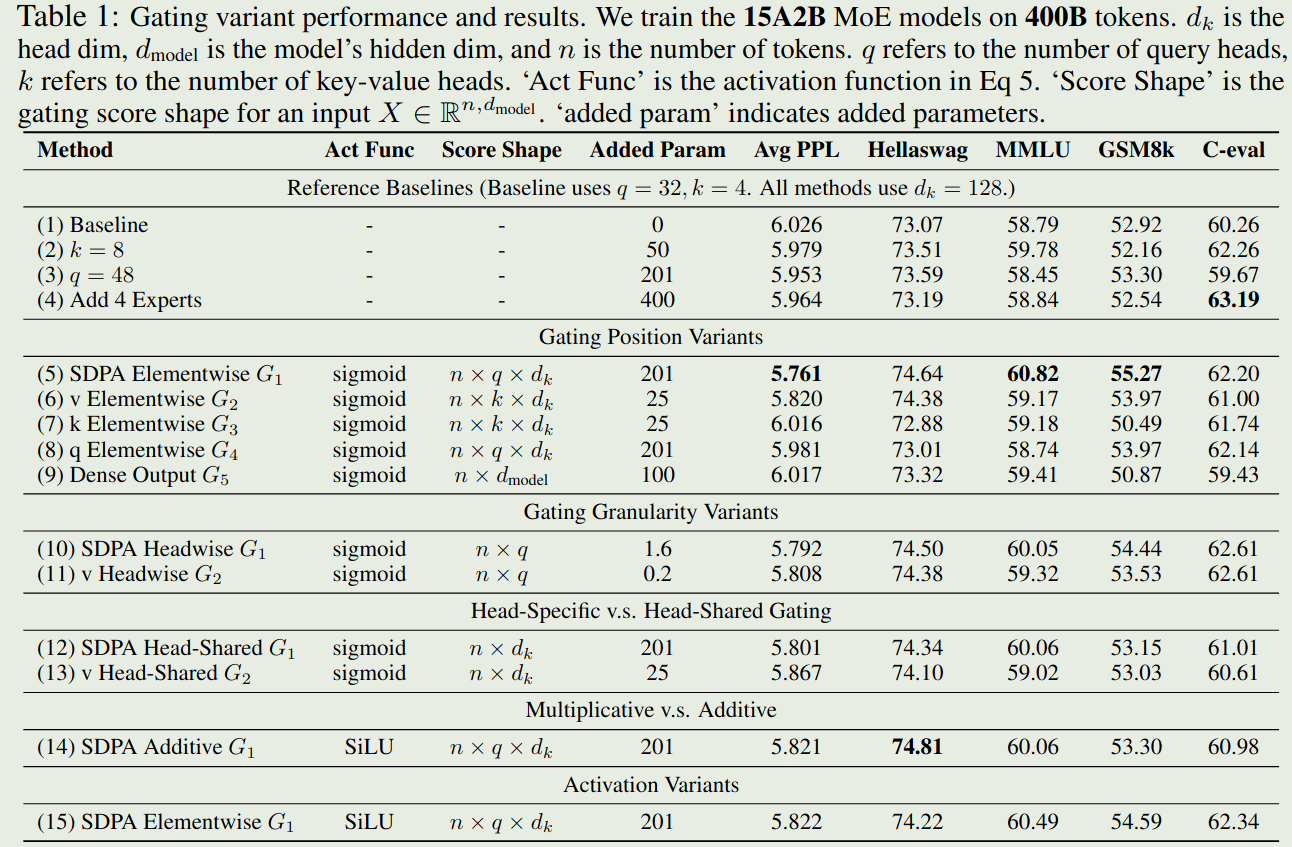
结论如下:
- 对 SDPA 的输出 (G1) 或者 value (G2) 进行 gating 效果最好
- head-specific gating 效果更好
- multiplication 效果比 addition 效果更好
- sigmoid 效果比 SiLU 效果更好
总的来说,position 对最终结果提升最明显,其次是 granularity 和 activation function.
接下来是不同 gating 方法对 dense model 的影响,作者构建了两个 dense 模型,参数都是 1.7B, 这两个模型的 layers 和 FFN hidden size 不同(通过调整保持总参数一致)。作者对比了 G1 和 baseline 的表现, 结果如下图所示
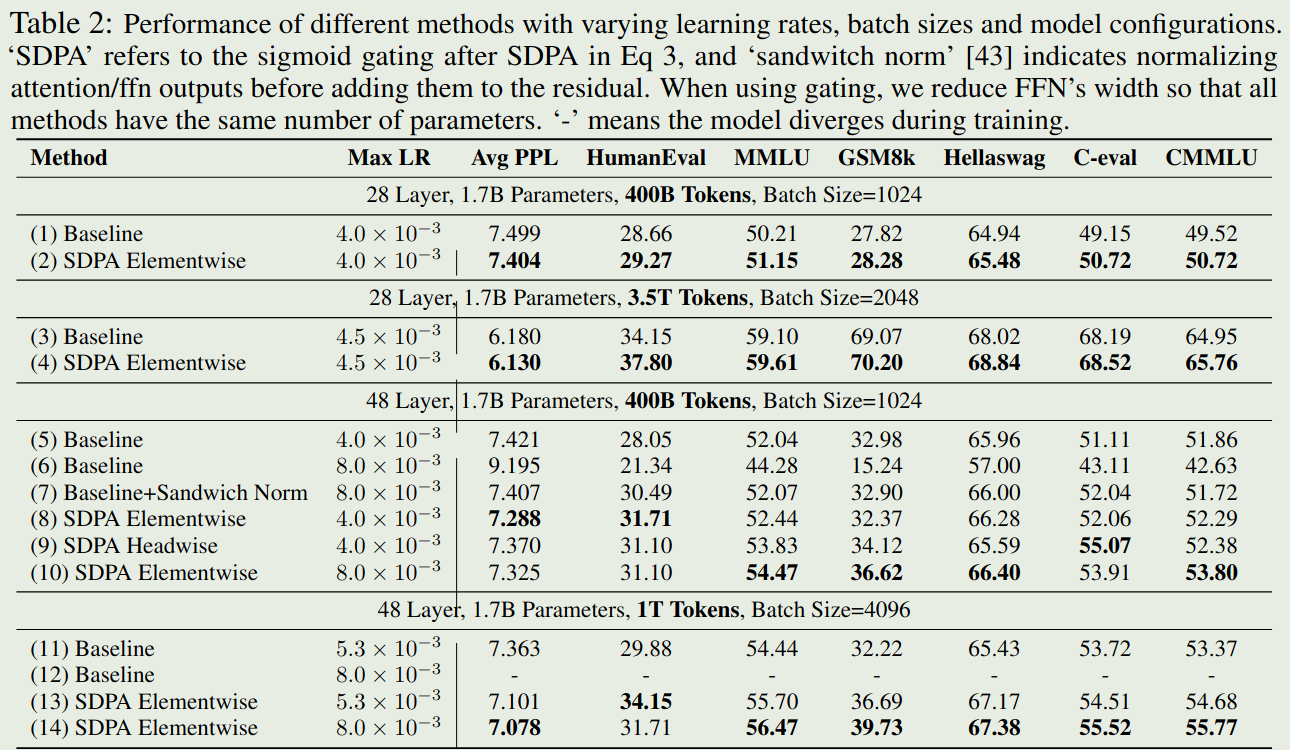
结论验证了 gating 机制可以有效提高模型的表现。作者还发现使用 gating 之后,模型的训练也更加稳定,训练的损失变化曲线如下图所示
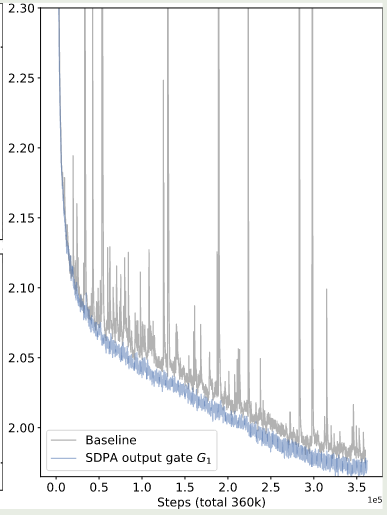
Analysis
首先,作者对 multi head attention 进行了重写,得到如下形式
$$ o_i^k = \sum_{j=1}^i\left(S_{ij}^k X_jW_V^k\right)W_O^k = \sum_{j=1}^i S_{ij}^k X_j(W_V^kW_O^k) $$也就是说,$W_K$ 和 $W_O$ 可以吸收到一起,由于 $W_V^j\in\mathbb{R}^{d\times d_k}$, $W_O^k\in\mathbb{R}^{d_k\times d}$, 从而 $\mathrm{rank}(W_V^jW_O^k)\leq \max(\mathrm{rank}(W_V^j), \mathrm{rank}(W_O^k))\leq d_k$. 对于 GQA 和 MQA, 最终的有效秩会进一步降低。
而使用本文提到的 G1 和 G2 gating 策略之后,我们相当于是通过非线性机制提高了上面的秩,进而解决了 softmax attention 表达能力不足的问题, 实际上,StepFun 的 MFA 也是类似的思想。下面是 G1 和 G2 做的改进:
$$ \begin{align} o_i^k &= \sum_{j=1}^i\left(S_{ij}^k \mathrm{gating}(X_jW_V^k)\right)W_O^k\tag{G1}\\ o_i^k &= \mathrm{gating}\left(\sum_{j=1}^iS_{ij}^k X_jW_V^k\right)W_O^k \tag{G2} \end{align} $$通过 gating 的非线性机制,我们提高的矩阵的秩,进而提高了模型的表达能力,而 G5 提升有限的原因也在于此。实验结果如下图所示
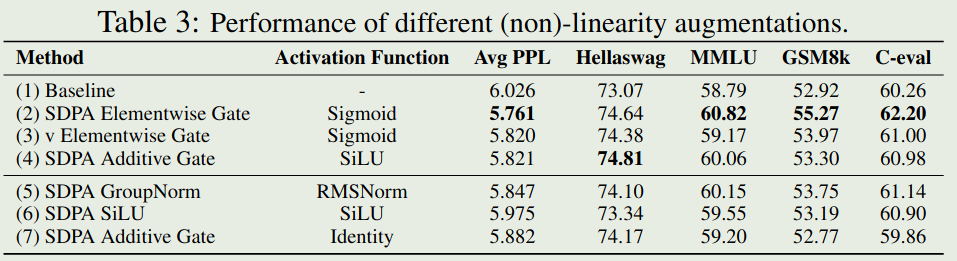
可以看到,不同的 non-linearity 方法对模型表现都有提升,这验证了矩阵秩会影响模型表达能力的分析。
接下来,作者探究了 gating 机制对 attention score distribution 的影响,结果如下图所示
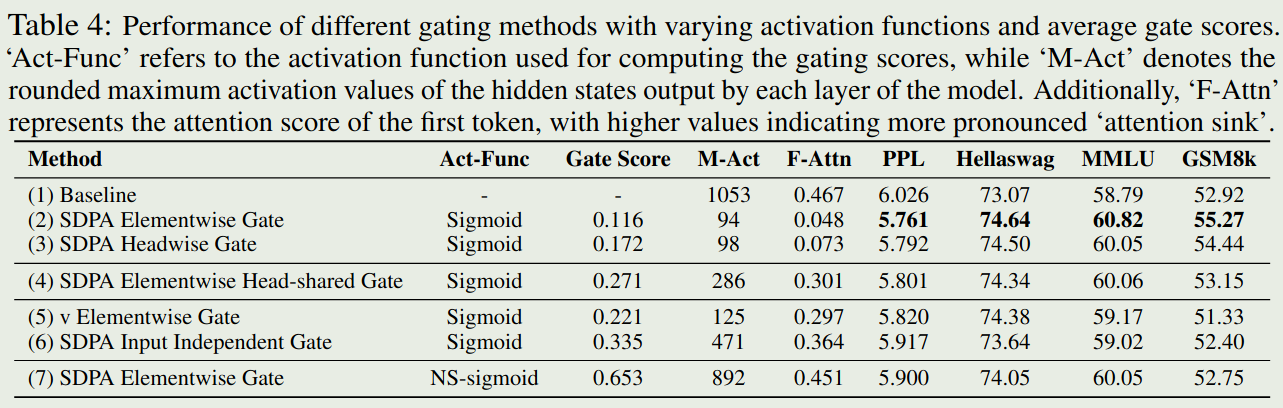
实验结果说明:
- 有效的 gating 机制对应的 attention score 是非常稀疏的
- head-specific sparsity 非常重要,当在不同的 head 共享 gating 时,模型表现会有所下降
- gating 必须与 query 相关,与 G2 先比,G1 的表现更好,这说明 gating score 更依赖于 query. 作者认为基于当前 query token 构建 gating, 可以有效过滤历史 token 的噪音信息
- non-sparse gating 效果比较差,作者构建了一个 non-sparse 版本的 sigmoid, 结果发现模型表现非常差,这说明了 attention score 应该是一个稀疏形式
通过前面的分析和实验结果,作者认为 gating 机制还可以缓解 attention sink 现象,作者对 baseline 以及 G1 两种方法的 attention 分布进行了可视化,结果如下图所示
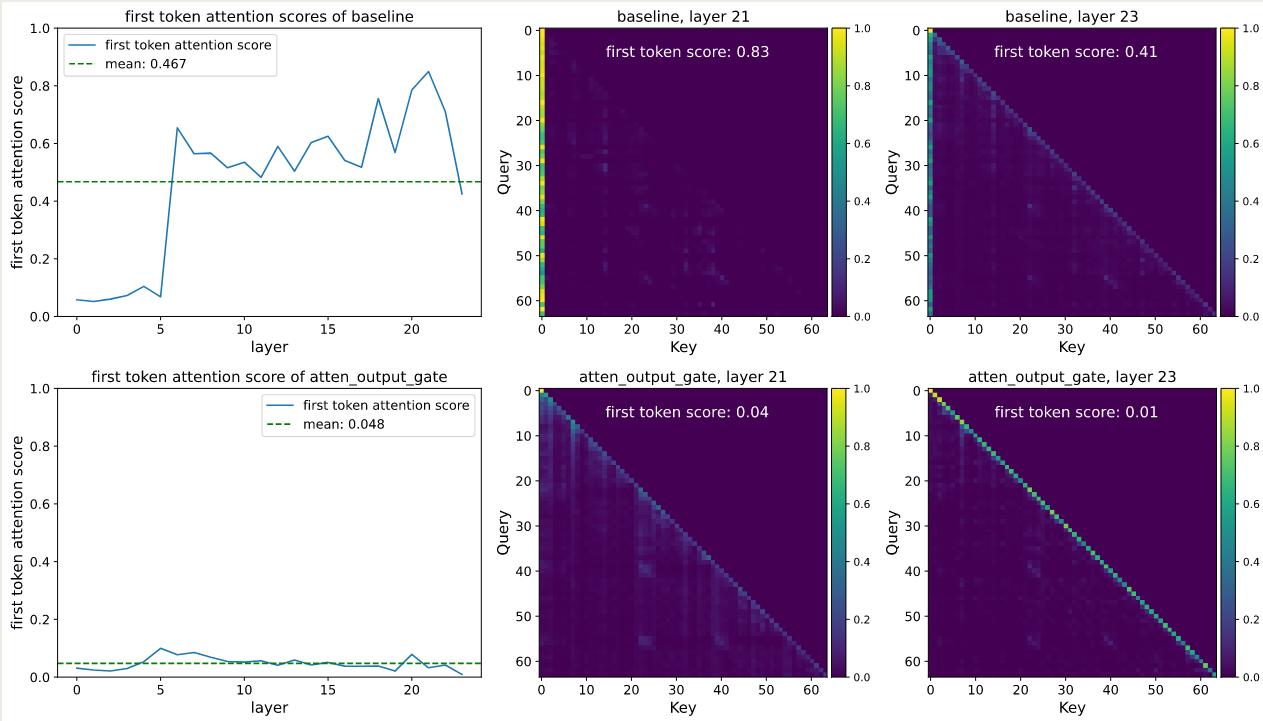
实验结果整理如下表所示
| method | massive activation | attention sink |
|---|---|---|
| baseline | high | high |
| input-independence | high | high |
| head-shared gating | low | high |
| head-specific gating | low | low |
因此,作者的结论为,input-dependent, head-specific gating 可以提高 attention score distribution 的 sparsity, 进而减缓 attention sink. 并且引入 spaisity 之后,我们还可以避免 massive activation, 进而使用更低的精度进行训练。
最后,作者探究了以下 gating 机制的上下文扩展能力,作者在已有的模型上基于 32k 上下文长度使用了 80B token 进行 continue pre-training, 然后使用 YARN 将模型上下文长度扩展到了 128K。 测试的结果如下图所示
| Method | 4k | 8k | 16k | 32k | 64k | 128k |
|---|---|---|---|---|---|---|
| Baseline | 88.89 | 85.88 | 83.15 | 79.50 | - | - |
| SDPA-Gate | 90.56 | 87.11 | 84.61 | 79.77 | - | - |
| YaRN Extended | ||||||
| Baseline | 82.90 (-6.0) | 71.52 (-14.4) | 61.23 (-21.9) | 37.94 (-41.56) | 37.51 | 31.65 |
| SDPA-Gate | 88.13 (-2.4) | 80.01 (-7.1) | 76.74 (-7.87) | 72.88 (-6.89) | 66.60 | 58.82 |
可以看到,对于短上下文,虽然两者表现都有所下降,但是本文提出的 gating 表现下降程度较小。而对于长上下文,本文提出的 gating 机制效果明显更好。作者分析原因认为这是由于 softmax attention 倾向于退化为对少数 token 的依赖, 而 gating 通过引入 token-level sparsity,避免了这种路径依赖。
Conclusion
在本文中,作者系统性探究了 attention 中的 gating 机制,包括 gating 对模型表现,训练稳定性以及训练动态的影响。作者发现,通过提高 non-linearity 和 sparsity 我们可以有效提高模型的上下文能力以及减缓 attention sink 现象。
从更高层次看,本文的结果可以总结为一点:
attention 的问题不在于 softmax 本身,而在于线性 aggregation 的表达上限与缺乏选择性。而 gating 提供了一种几乎零成本、却极其有效的方式来引入非线性与稀疏性。
References
Appendix
作者在附录中还进一步分析了 massive activation 以及 attention sink.
- massive activation 并不是 attention sink 产生的必要原因,并且 sparsity 可以减缓这一现象
- head-specific gating 会提升 gating score 的值,因此不同的 head 需要安排不同的 sparsity
- 并不能通过 clipping 的方式来提高训练稳定性
- 在 continue pre-training 阶段加入 gating 机制并不能提高模型的表现