Introduction
在本节中,我们先介绍 KL divergence 的基本定义,然后我们介绍 KL divergence 的一般形式,即 f-divergence.
KL-divergence
KL divergence 用于衡量近似概率分布 $Q(x)$ 到真实概率分布 $P(x)$ 的误差,我们可以将其理解为:如果我们用 $Q(x)$ 来替换 $P(x)$, 会有多大的信息损失?
连续概率分布的 KL divergence 的定义如下
$$ D_{KL}(P\parallel Q) =\mathbb{E}_{x\sim P}\left[\log \frac{P(x)}{Q(x)}\right]=\int P(x)\log\left(\frac{P(x)}{Q(x)}\right)dx $$离散概率分布的 KL divergence 定义如下
$$ D_{KL}(P\parallel Q) = \sum_{x} P(x)\log\left(\frac{P(x)}{Q(x)}\right) $$KL divergence 有两几个关键性质:
- 非负性:$D_{KL}(P\parallel Q)\geq0$, 且 $D_{KL}(P\parallel Q)=0$ 当且仅当 $P(x)=Q(x)$ 对任意 $x$ 成立
- 非对称性: 一般情况下,$D_{KL}(P\parallel Q)\neq D_{KL}(Q\parallel P)$.
- 有限性:如果存在 $x$ 使得 $P(x)>0$ 但是 $Q(x)=0$, 则 $D_{\mathrm{KL}}(P\parallel Q)=\infty$.
一般我们称 $D_{KL}(P\parallel Q)$ 为 forward KL (相对于 $Q$), 对应的还有 reverse KL $D_{KL}(Q\parallel P)$ (相对于 $Q$).
F-divergence
KL divergence 是 f-divergence 的一种特殊情况。 f-divergence 是一类衡量不同概率分布 $P$ 和 $Q$ 的函数 $D_f(P\parallel Q)$.
假设函数 $f:(0,\infty)\to\mathbb{R}$ 是一个凸函数,且 $f(1)=0$. $P$ 和 $Q$ 是两个概率分布,则 f-divergence 定义如下
$$ D_f(P\parallel Q) = \mathbb{E}_{x\sim Q}\left[ f\left(\frac{P(x)}{Q(x)}\right)\right]=\int Q(x)f\left(\frac{P(x)}{Q(x)}\right)dx $$我们称 $f$ 为 $D_f$ 的 generator.
以下是几种常见的 f-divergence:
| Name | generator |
|---|---|
| forward KL divergence | $f(x)=x\log x$ |
| reverse KL divergence | $f(x)=-\log x$ |
| Total variation | $f(x)=1/2\vert x-1\vert$ |
| $\chi^2$-divergence | $f(x)=(x-1)^2$ |
| JS-divergence | $f(x)=x\log\frac{2x}{x+1}+\log\frac{2}{x+1}$ |
我们这里推导一下 KL divergence 对应的 generator.
对于 forward KL, 注意到
$$ D_f(P \parallel Q) = \int Q(x) \left( \frac{P(x)}{Q(x)} \log \frac{P(x)}{Q(x)} \right) dx = \int P(x) \log \frac{P(x)}{Q(x)} dx = D_{KL}(P \parallel Q) $$因此 forward KL 对应的 generator 为 $f=x\log x$.
对于 reverse KL, 注意到
$$ D_f(P \parallel Q) = \int Q(x) \left( -\log \frac{P(x)}{Q(x)} \right) dx = \int Q(x) \log \frac{Q(x)}{P(x)} dx = D_{KL}(Q \parallel P) $$因此 forward KL 对应的 generator 为 $f=-\log x$.
Properties of F-divergence
f-divergence 性质如下
- linearity: $D_{a_1f_1+a_2f_2}=a_1D_{f_1}+a_2D_{f_2}$.
- $D_f=D_g$ 当且仅当存在 $c\in\mathbb{R}$ 使得 $f(x)=g(x)+c(x-1)$.
- non-negativity. $D_f(P\parallel Q)\geq0$ 且 $D_f(P\parallel Q)$ 当且仅当 $P=Q$.
性质 2 证明如下:
如果 $f(x)=g(x)+c(x-1)$, 则通过定义,我们可以验证得到 $D_f=D_g$.
反之,如果 $D_f=D_g$, 令 $h=f-g$, 对任意两个在集合 $\{0, 1\}$ 上的概率分布 $P,Q$, 由于 $D_f(P\parallel Q) - D_g(P\parallel Q)=0$, 我们有
$$ h\left(\frac{P(1)}{Q(1)}\right) = -\frac{Q(0)}{Q(1)}h\left(\frac{P(0)}{Q(0)}\right) $$我们不妨假设 $P(0)=aQ(0)$, $P(1)=bQ(1)$, 结合 $P(0)+P(1)=1$ 和 $Q(0)+Q(1)=1$ 我们有
$$ Q(0) = \frac{1-a}{b-a}, Q(1) = \frac{b-1}{b-a} $$从而
$$ \frac{h(b)}{b-1}=\frac{h(a)}{a-1} $$由于我们可以任意选定 $P$ 和 $Q$, 因此 $h$ 是一个线性函数,形式为 $h(x)=c(x-1)$. $\blacksquare$
Approximation
本节中,我们将介绍针对 KL divergence 的三种近似形式。
在实际计算 KL divergence 时,由于:
- 完整计算 KL divergence 需要的算力或内存过高
- 没有闭式解
- 我们可以仅保存 log-probability, 而不是整个概率分布
因此,我们假设我们只能计算输入 $x$ 对应的概率 $P(x)$ 和 $Q(x)$. 一般来说,我们会通过 Monte Carlo estimate 来进行近似。即我们先对 $P$ 进行采样得到 $x_1,\dots,x_N\sim P$, 然后我们构建估计量。
一个高的估计量应该是无偏 (unbiased) 并且方差低 (low variance) 的。John Schulman 给出了三种 estimator. 我们分别针对 forward KL 和 reverse KL 进行介绍。这里我们定义
$$ r = \frac{P(x)}{Q(x)} $$Forward KL Estimation
对于 forward KL $D_{KL}(P\parallel Q)$, 其对应的 generator 为 $f(x)=x\log x$, 注意到 $\mathbb{E}_{x\sim Q}[r]=1$, 且 $f$ 是一个凸函数,因此我们有 $f(r)-f'(1)(r-1)\geq0$, 从而我们可以得到一个新的估计为 $\boxed{k=r\log r - (r-1)}$.
Reverse KL Estimation
对于 reverse KL $D_{KL}(Q\parallel P)$, 其对应的 generator 为 $f(x)=-\log x$, 由概率性质,$\boxed{k_1=-\log r}$ 是 $D_{KL}(Q\parallel P)$ 的一个无偏估计。但是 $k_1$ 的问题在于 当 $r$ 非常小时,$k_1$ 会变得非常大。也就是说,$k_1$ 的 variance 比较高。
John Schulman 基于 f-divergence 泰勒展开给出了一个新的估计 $k_2$, 其定义为
$$ \boxed{k_2 = \frac12(\log r)^2} $$其期望为
$$ \mathbb{E}_Q[k_2] = \mathbb{E}_Q\left[\frac12(\log r)^2\right] $$这是一个 f-divergence, 对应的 generator 为 $f_{k_2}(x)=1/2(\log x)^2$, 而 $D_{KL}(Q\parallel P)$ 对应的 generator 为 $f_{k_1}(x)=-\log x$.
当 $P$ 和 $Q$ 比较靠近时,我们记 $\theta=r-1$, 对 $D_{f}(P\parallel Q)$ 在 $x=1$ 处进行展开得到
$$ \begin{aligned} D_f(P\parallel Q) &= \mathbb{E}_{x\sim Q}\left[ f(r)\right]\\ &= \mathbb{E}_{x\sim Q}\left[ f(1) + f'(1)\theta + \frac{f''(1)}{2}f(1+\lambda)\theta^2+O(\theta^3)\right]\\ &= \frac{f''(1)}{2}F\theta^2+O(\theta^3) \end{aligned} $$这里我们应用了 $f(1)=0$, $\mathbb{E}[\theta]=0$, $F=\mathbb{E}[f(1+\lambda\theta)$ 是 Fisher information matrix.
我们分别带入 $f_{k_1}(x)$ 和 $f_{k_2}(x)$ 得到 $f_{k_1}''(1)=f_{k_2}''(1)=1$, 即 $k_1$ 和 $k_2$ 在 $P$ 和 $Q$ 比较靠近时二阶近似是相同的。因此,**$k_2$ 表面上是一个二阶近似,在分布接近时有效,但本质上是在优化 另一个 f-divergence*
John Schulman 还构造了第三种估计。回顾前面 f-divergence 的性质 2,即当 $f(x)=g(x)+c(x-1)$ 时,我们有 $D_f=D_g$, 因此我们可以选取合适的 $c$ 来降低估计的 variance. 注意到 $k_1$ 的主要问题在于存在负数的可能性,因此我们就构建一个对应的估计量来解决这个问题。注意到 $\log x \leq x -1$, 因此我们可以令 $c=1$, 此时就得到了新的估计
$$ \boxed{k_3 =(r-1)- \log r } $$$k_3$ 继承了 $k_1$ 的无偏性,并且 $k_3$ 通过 f-divergence 等价类消除了负值,兼顾无偏与低方差,解决了 $k_1$ variance 过大的问题
Experiments on Approximation
对于分布 $P=\mathcal{N}(0,1)$ 以及 $Q=\mathcal{N}(0.1, 1)$, 真实的 KV divergence 为 0.005, 三个 estimator 的误差如下表所示
| Method | Bias | Std Dev |
|---|---|---|
| $k_1$ | 0.0001 | 20.0005 |
| $k_2$ | 0.0025 | 1.4175 |
| $k_3$ | 0.0000 | 1.4163 |
当 $P=\mathcal{N}(1,1)$, $Q=\mathcal{N}(0.1, 1)$ 时, 真实的 KV divergence 为 0.405, 三个 estimator 的误差如下表所示
| Method | Bias | Std Dev |
|---|---|---|
| $k_1$ | -0.0000 | 2.2223 |
| $k_2$ | 0.2025 | 1.6762 |
| $k_3$ | 0.0000 | 1.6342 |
可以看到 $k_1$ 的 variance 非常大,$k_2$ 是一个有偏估计,$k_3$ 既满足了无偏又满足了 low variance.
Summary
我们接下来总结 reverse KL $D_{KL}(Q\parallel P)$ 的近似 $k_1$, $k_2$ 和 $k_3$ 的性质如下 ($r=P(x)/Q(x)$)
| estimation | definition | motivation | bias | variance |
|---|---|---|---|---|
| $k_1$ | $-\log r$ | naive estimation | unbiased | high |
| $k_2$ | $\frac12(\log r)^2$ | f-divergence, taylor expansion | biased | low |
| $k_3$ | $(r-1)- \log r$ | f-divergence, non-negativity | unbiased | low |
Applications to ML
Remark 本节内容主要参考了 KL Divergence for Machine Learning
我们假设真实目标分布和近似的目标分布分别记为 $p_{data}(x)$ 和 $p_\theta(x)$. 由于 KL divergence 的非对称性,因此我们需要考虑两种目标函数:
- forward KL: $\arg\min_\theta D_{KL}(p_{data}\parallel p_\theta)$
- reverse KL: $\arg\min_\theta D_{KL}(p_\theta \parallel p_{data})$
我们将会看到,这两种不同的目标函数导致的结果也不尽相同
Forward KL
对目标函数进行简化得到
$$ \arg\min_\theta D_{KL}(p_{data}\parallel p_\theta) = \arg\max_\theta \mathbb{E}_{x\sim p_{data}}\left[\log p_\theta(x)\right] $$实际在计算时,我们会使用 Monte Carlo 的方式对真实分布进行采样然后进行估计。
Forward KL 其代表的含义为,我们从分布 $p_{data}$ 中进行采样,然后求 $p_\theta$ 的最大似然估计。最终的结果满足:当 $p_{data}(x)$ 概率很高时,$p_\theta(x)$ 的概率也需要很高. 这是一种 mean-seeking behavior, 因为 $p_\theta$ 必须覆盖 $p_{data}$ 的所有 modes.
一般来说,supervised learning 对应的就是 forward KL. 我们可以证明 forward KL divergence 和 MLE 是等价的。也就是说,最大似然估计得到的分布就是 KL divergence 最小的近似分布。我们将 $p_{data}(x)$ 和 $p_\theta(x)$ 对应的 KL divergence 进行展开得到
$$ \begin{aligned} \theta_{KL}^* &= \arg\min_{\theta}D_{KL}(p_{data}(x)\parallel p_\theta(x))\\ &= \arg\min_{\theta} \int p_{data}(x)\frac{p_{data}(x)}{p_\theta(x)} dx\\ &= \arg\min_{\theta}\int p_{data}(x)\log p_{data}(x) dx - \int p_{data}(x)\log p_\theta(x)dx \\ &= \arg\min_{\theta} - \int p_{data}(x)\log p_\theta(x)dx \\ &= \arg\max_{\theta} \int p_{data}(x)\log p_\theta(x)dx \end{aligned} $$实际上,真实的数据分布 $p_{data}(x)$ 是未知的,我们只有从 $p_{data}(x)$ 采样得到的一批数据 $X=\{x_1,\dots,x_n\}\sim p_{data}(x)$. 基于大数定律,我们有
$$ \frac{1}{n}\sum_{i=1}^n\log p(\theta_i\mid \theta)=\mathbb{E}_{x\sim p_{data}}[\log p_\theta(x)] = \int p_{data}(x)\log p_\theta(x)dx, n\to \infty $$这样,最大似然估计就与最小化 KL divergence 构建起了联系:
$$ \begin{aligned} \theta_{MLE}^*&=\arg\max_{\theta} \sum_{i=1}^n \log p(x_i\mid \theta)\\ &= \arg\max_{\theta} \int p_{data}(x)\log p_\theta(x)dx\\ &= \theta_{KL}^*, n\to\infty. \end{aligned} $$也就是说,当采样样本足够多的时候,最大似然估计和最小 KL divergence 是等价的。监督学习中,我们先从真实分布 $p_{data}(x,y)$ 中收集一个数据集 $\mathcal{D}=\{(x_i,y_i)\}$, 然后我们会基于模型 $f_\theta:\mathcal{X}\to\mathcal{Y}$ 和损失函数 $\mathcal{L}:\mathcal{Y}\times\mathcal{Y}\to\mathbb{R}$ 来优化模型参数 $\theta$:
$$ \arg\min_\theta \mathbb{E}_{(x_i,y_i)\sim\mathcal{D}}[\mathcal{L}(f_\theta(x_i), y_i)] $$对于使用 cross-entropy loss 的分类问题以及 MSE loss 的回归问题,其目标函数实际上都是最小化 KL divergence.
Reverse KL
对目标函数进行简化,得到
$$ \arg\min_\theta D_{KL}(Q_\theta\parallel p_{data}) = \arg\max_\theta \mathbb{E}_{x\sim Q_\theta}\left[\log p_{data}(x)\right] - \mathbb{E}_{x\sim Q_\theta}\left[\log Q_\theta(x)\right] $$实际在计算时,我们需要知道真实概率分布在采样点上的概率值 $p_{data}(x)$.
Reverse KL 代表的含义为,我们从分布 $p_\theta(x)$ 中进行采样,然后最大化采样点在 $p_{data}(x)$ 中的概率分布。entropy item 鼓励 $p_\theta$ 尽可能均匀分布(覆盖广),从而最终结果满足:当 $p_\theta(x)$ 概率很高时,$p_{data}(x)$ 的概率也需要很高。注意到与 forward KL 不同,Reverse KL 中包含 entropy 项,其避免了 $p_\theta$ 收缩到 $p_{data}$ 的某一个 非常窄的 mode 上,最终结果是 $p_\theta$ 会找到 $p_{data}$ 的一个 high probability 以及 wide support 的 mode, 然后进行覆盖。
一般来说,reinforcement learning 对应的就是 reverse KL, 这是因为我们希望 policy model 不要离 reference model 太远,并不一定要 cover 所有的 mode.
Experiments on forward and Reverse KL
我们通过概率分布来可视化 forward RL 与 reverse RL 的区别,验证 forward KL 与 reverse KL 不同的模式。
我们假设 $p_{data}=w_1\mathcal{N}(\mu_1, \sigma_1^2)+w_2\mathcal{N}(\mu_2, \sigma_2^2)$, 然后我们用一个 normal distribution $p_\theta=\mathcal{N}(\mu, \sigma^2)$ 来近似 $p_{data}$, 这里 $\theta=(\mu, \sigma^2)$. 对于 forward KL, 我们可以从理论上得出最优解,对应的 $\mu=w_1\mu_1+w_2\mu_2$, 而 reverse KL 则只能通过优化的方式进行求解,并且解与初始化条件相关,下面是相关的实验结果
首先我们令 $w_1=w_2=0.5$, $\mu_1=\mu_2=4.0$, $\sigma_1=\sigma_2=1$, reverse KL 的初始化条件为 $\theta_0=(2,1)$, 对应的结果为
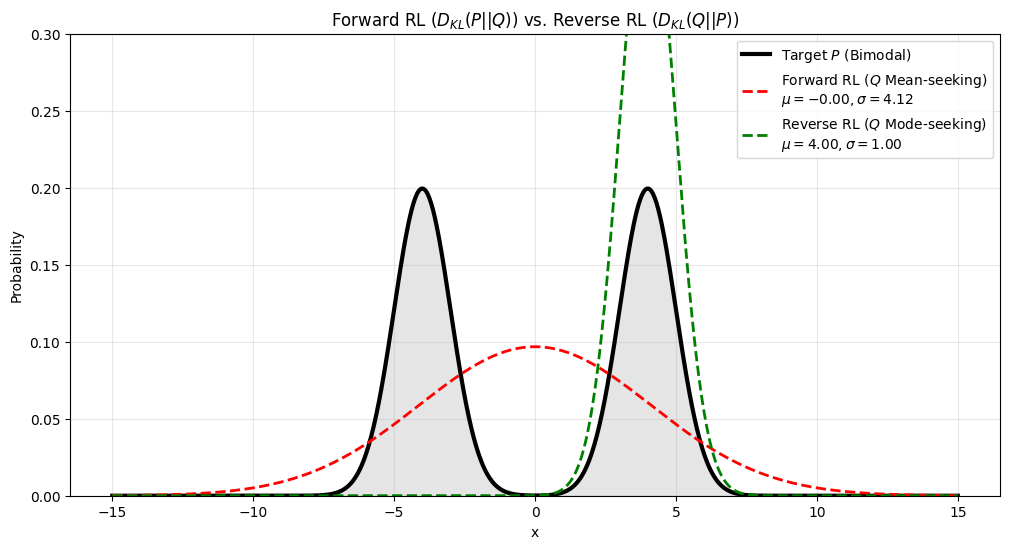
接下来我们改变 reverse KL 的初始化条件为 $\theta_0=(-2,1)$, 对应的结果为
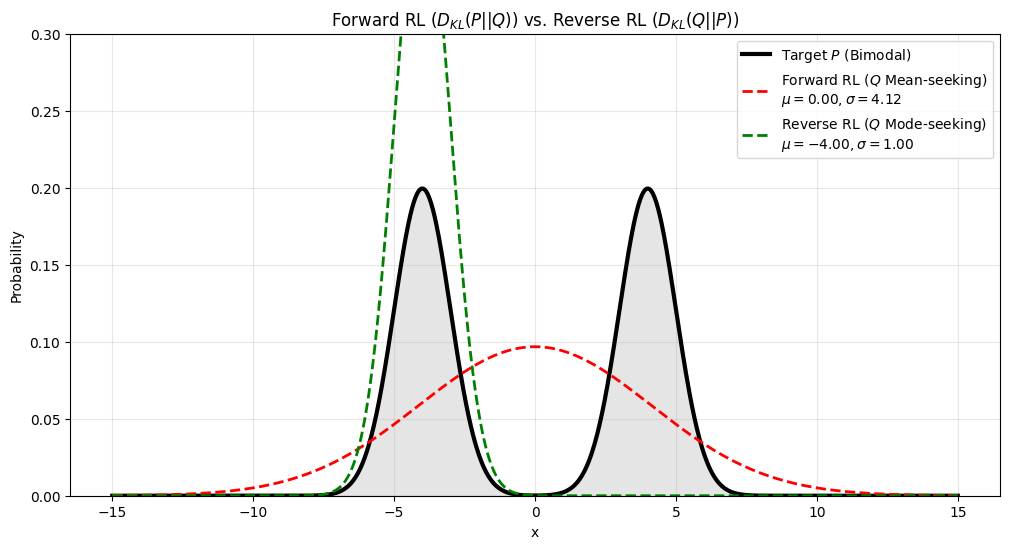
可以看到,与前面分析一致,使用 forward KL 时,最终得到的 $p_\theta$ 会倾向于拟合分布的中心 (mean seeking), 即 $\mu(p_\theta)=\mu(p_{data})$, 而使用 reverse KL 时,最终得到的 $P$ 会倾向于拟合分布的 mode (mode seeking).
Applications to RL
Remark 本节内容主要参考了 Understanding KL Divergence Estimators in RL: From Value Approximation to Gradient Estimation
在本节中,我们将基于 RL 来推导 KL 的相关性质。为了统一,这里我们使用 RL 中常见的 notation 来进行计算
| notation | description |
|---|---|
| $\pi_\theta$ | policy model with parameter $\theta$ |
| $\pi_{ref}$ | reference model |
| $\pi_{old}$ | behavior model to sample from |
| $s_\theta(x)=\nabla_\theta \log \pi_\theta(x)$ | score function |
| $\rho(x)=\pi_\theta(x)/\pi_{old}(x)$ | importance weight |
| $\mathrm{sg}(\cdot)$ | stop gradient operation |
首先 score function 有一个期望为 0 的性质:
$$ \mathbb{E}_{x\sim\pi_\theta}[s_\theta(x)]=\int_x \pi_\theta(x)\nabla_\theta \log \pi_\theta(x)dx = \int_x\nabla_\theta \pi_\theta(x)dx= \nabla_\theta\int_x \pi_\theta(x)dx =\nabla_\theta1 = 0 $$接下来,我们分别推导 forward KL 和 reverse KL 的梯度。对于 forward KL, 我们有
$$ \nabla_\theta D_{KL}(\pi_{ref}\parallel \pi_\theta) = -\int \pi_{ref}\nabla_\theta \log \pi_\theta dx=-\mathbb{E}_{\pi_{ref}}[s_\theta] = \boxed{-\mathbb{E}_{\pi_\theta}\left[\frac{\pi_{ref}}{\pi_\theta}s_\theta\right]} $$对于 reverse KL,我们有
$$ \begin{aligned} \nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})& = \int\left[\nabla_\theta \pi_\theta\cdot\log\frac{\pi_\theta}{\pi_{ref}} + \pi_\theta \nabla_\theta\log \frac{\pi_\theta}{\pi_{ref}}\right]dx\\ &= \int \pi_\theta s_\theta\log \frac{\pi_\theta}{\pi_{ref}}dx + \int \pi_\theta s_\theta dx\\ &= \mathbb{E}_{\pi_\theta}\left[s_\theta\log \frac{\pi_\theta}{\pi_{ref}}\right]+\mathbb{E}_{\pi_\theta}[s_\theta]\\ &= \boxed{\mathbb{E}_{\pi_\theta}\left[s_\theta\log \frac{\pi_\theta}{\pi_{ref}}\right]} \end{aligned} $$这里我们使用了 $\nabla_\theta\pi_\theta=\pi_\theta s_\theta$ , $\nabla_\theta\log\pi_\theta=s_\theta$ 以及 前面推导的 $\mathbb{E}_{\pi_\theta}[s_\theta]=0$ 的结论.
RL 的目标函数如下
$$ \mathcal{J}(\theta) = \mathbb{E}_{\tau\sim \pi_\theta}\left[\sum_{t=0}^T\gamma^tr(s_t,a_t)\right] - \beta D_{KL}(\pi_\theta\parallel \pi_{ref}) $$Ki as Loss
由于 KL divergcne 不能直接计算(或者计算难度较大),因此,基于前面对 KL divergence estimation 的分析,我们可以使用如下代理损失函数来优化我们的模型:
$$ \mathcal{J}_1(\theta) = \mathbb{E}_{\tau\sim \pi_\theta}\left[\sum_{t=0}^T\gamma^tr(s_t,a_t)\right] - \beta k_i(\pi_\theta, \pi_{ref}) $$这里 $i\in\{1,2,3\}$ 代表了我们使用的估计。从直觉上来说,这样做是没问题的,但是我们将从数学分析上说明,$k_1,k_3$ 作为损失函数都存在问题。其核心问题在于
$$ \mathbb{E}[\widehat{D_{KL}}]=D_{KL} \nRightarrow \mathbb{E}[\nabla_\theta \widehat{D_{KL}}] =\nabla_\theta D_{KL} $$也就是说,KL divergence estimation 的无偏性不能推导出 KL divergence estimation gradient 的无偏性,这是因为我们在求期望时,对应的概率分布可能也与参数相关。实际上,我们有
$$ \begin{aligned} \nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref}) &= \nabla_\theta \mathbb{E}_{x\sim\pi_\theta}[\widehat{D_{KL}}(\pi_\theta\parallel \pi_{ref})]\\ &= \mathbb{E}_{x\sim\pi_\theta}[\nabla_\theta \widehat{D_{KL}}(\pi_\theta\parallel \pi_{ref})] + \mathbb{E}_{x\sim\pi_\theta}[\widehat{D_{KL}}(\pi_\theta\parallel \pi_{ref})\nabla_\theta \pi_\theta(x)]\\ &\neq \mathbb{E}_{x\sim\pi_\theta}[\nabla_\theta \widehat{D_{KL}}(\pi_\theta\parallel \pi_{ref})] \end{aligned} $$因此 $\nabla_\theta \widehat{D_{KL}}$ 是 $\nabla_\theta D_{KL}$ 的一个有偏估计。
我们分别来分析一下 $k_1,k_2,k_3$ 梯度,
$$ \begin{aligned} \nabla_\theta k_1 &= \nabla_\theta\left[-\log \frac{\pi_{ref}}{\pi_\theta}\right] = s_\theta\\ \nabla_\theta k_2 &= \nabla_\theta\left[\frac12\left(\log \frac{\pi_{ref}}{\pi_\theta}\right)^2\right] = -\log \frac{\pi_{ref}}{\pi_\theta}s_\theta\\ \nabla_\theta k_3 &= \nabla_\theta\left[\frac{\pi_{ref}}{\pi_\theta}-1- \log \frac{\pi_{ref}}{\pi_\theta}\right] = \left(1 - \frac{\pi_{ref}}{\pi_\theta}\right)s_\theta \end{aligned} $$此时对应的梯度的期望为
$$ \begin{aligned} \mathbb{E}_{\pi_{\theta}}[\nabla_\theta k_1] &= \mathbb{E}_{\pi_{\theta}}[s_\theta]=0\\ \mathbb{E}_{\pi_{\theta}}[\nabla_\theta k_2] &= \mathbb{E}_{\pi_{\theta}}\left[-\log \frac{\pi_{ref}}{\pi_\theta}s_\theta\right]=\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})\\ \mathbb{E}_{\pi_{\theta}}[\nabla_\theta k_3] &= \mathbb{E}_{\pi_{\theta}}\left[\left(1 - \frac{\pi_{ref}}{\pi_\theta}\right)s_\theta\right]=\nabla_\theta D_{KL}(\pi_{ref}\parallel \pi_\theta)\\ \end{aligned} $$也就是说,$k_1$ 估计的梯度的期望为 0,对整体训练没有任何帮助,$k_3$ 估计的梯度的期望等价于优化 forward KL, **只有 $k_2$ 估计的梯度的期望等价于优化 reverse KL.
在实际代码实现的时候,KL divergence 有两种不同的实现形式:
第一种是根据定义将 KL divergence 作为损失函数的一部分,此时我们的 KL divergence 参与反向传播,对应的实现方式如下
| |
第二种是只调整 reward, 而不参与反向传播(通过 $\mathrm{sg}(\cdot)$ 实现),对应的实现方式如下所示
| |
这两者对于模型的训练影响很大,下面我们分别来进行介绍
KL as Loss
为了统一 on-policy 和 off-policy 两种形式,我们使用一个统一的表达形式,即
$$ L=\rho k_i $$此时对应的 RL 目标函数为
$$ \mathcal{J}_2(\theta) = \mathbb{E}_{\tau\sim \pi_\theta}\left[\sum_{t=0}^T\gamma^tr(s_t,a_t)\right] - \beta\rho k_i(\pi_\theta, \pi_{ref}) $$这里
$$ \rho = \frac{\pi_\theta}{\mathrm{sg}(\pi_{old})} $$是 importance weight,
- 当算法为 on-policy 时,$\pi_\theta=\pi_{old}$, $\rho\equiv1$.
- 当算法为 off-policy 时,$\rho=\pi_\theta/\pi_{old}$, $\nabla_\theta \rho=\rho s_\theta$.
通过这种方式,我们使得参数分布本身不会对梯度计算产生影响,从而使得对期望进行求导和对导数求期望相等,即
$$ \nabla_\theta\mathbb{E}_{\pi_{old}}[k] = \int \pi_{old}(x)\nabla_\theta kdx= \mathbb{E}_{\pi_{old}}[\nabla_\theta k] $$接下来我们来计算对应估计的梯度的期望,即 $\mathbb{E}[\nabla_\theta(\rho k_i)]$, 首先我们计算对应的梯度
$$ \begin{aligned} \nabla_\theta (\rho k_1) &= \rho s_\theta k_1+r\rho_\theta=\rho s_\theta(k_1+1)\\ \nabla_\theta (\rho k_2) &= \rho s_\theta k_2+\rho\left(-\log \frac{\pi_{ref}}{\pi_\theta}s_\theta\right)=\rho s_\theta(k_1+k_2)\\ \nabla_\theta (\rho k_3) &= \rho s_\theta k_3+\rho\left(1 - \frac{\pi_{ref}}{\pi_\theta}\right)s_\theta=\rho s_\theta\left(k_3+1-\frac{\pi_{ref}}{\pi_\theta}\right)=\rho s_\theta k_1 \end{aligned} $$注意到 $\mathbb{E}_{\pi_{old}} [\rho k_i]=\mathbb{E}_{\pi_{\theta}}[k_i]$ 以及 $\mathbb{E}_{\pi_{\theta}}[s_\theta]=0$, 我们对上述梯度求期望得到
$$ \begin{aligned} \mathbb{E}_{\pi_{old}}[\nabla_\theta (\rho k_1)] &= \mathbb{E}_{\pi_{old}}[\rho s_\theta(k_1+1)]=\mathbb{E}_{\pi_{\theta}}[s_\theta k_1]=\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})\\ \mathbb{E}_{\pi_{old}}[\nabla_\theta (\rho k_2)] &= \mathbb{E}_{\pi_{old}}[\rho s_\theta(k_1+k_2)]=\nabla_\theta \mathbb{E}_{\pi_\theta}[k_2]\\ \mathbb{E}_{\pi_{old}}[\nabla_\theta (\rho k_3)] &= \mathbb{E}_{\pi_{old}}[\rho s_\theta k_1]=\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref}) \end{aligned} $$这里在计算 $\mathbb{E}_{\pi_{old}}[\nabla_\theta (\rho k_2)]$ 时,我们使用了 Leibniz 乘法法则:
$$ \mathbb{E}_{\pi_{old}}[\rho s_\theta(k_1+k_2)]= \mathbb{E}_{\pi_{\theta}}[s_\theta k_2]+\mathbb{E}_{\pi_{\theta}}[\nabla_\theta k_2]=\nabla_\theta\mathbb{E}_{\pi_{\theta}}[k_2] $$可以看到,$\rho k_1$ 和 $\rho k_3$ 都满足梯度与期望的可交换性,而 $\rho k_2$ 不满足,为了解决这个问题,我们可以使用 stop gradient, 即 $\mathrm{sg}(\rho)l_2$, 此时,我们有
$$ \nabla_\theta(\mathrm{sg}(\rho) k_2) = \mathrm{sg}(\rho)\nabla_\theta k_2 = \rho s_\theta k_1 $$对其求期望有
$$ \mathbb{E}_{\pi_{old}}[\nabla_\theta(\mathrm{sg}(\rho) k_2)] = \mathbb{E}_{\pi_{old}}[\rho s_\theta k_1] = \mathbb{E}_{\pi_{\theta}}[s_\theta k_1]=\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref}) $$我们将如上结果总结为下表
| Loss | gradient | expected gradient | objective |
|---|---|---|---|
| $\rho k_1$ | $\rho s_\theta (k_1+1)$ | $\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})$ | reverse KL |
| $\rho k_2$ | $\rho s_\theta (k_1+k_2)$ | $\nabla_\theta\mathbb{E}_{\pi_{\theta}}[k_2]$ | f-divergence |
| $\mathrm{sg}(\rho) k_2$ | $\rho s_\theta k_1$ | $\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})$ | reverse KL |
| $\rho k_3$ | $\rho s_\theta k_1$ | $\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})$ | reverse KL |
接下来,我们就可以分析在 on-policy 和 off-policy 场景下分析不同 estimator 的性质了。
如果说,我们显式加入 $\rho$, 则根据上表我们可以使用上表的 $\rho k_1$, $\mathrm{sg}(\rho) k_2$ 以及 $\rho k_3$ 都可以作为损失函数的代替。
注 实际上 on-policy 场景下使用 $k_2$ 也有用的原因在于 $\nabla_\theta k_2=s_\theta k_1$, 也就是 $k_2$ 和 $\rho k_3$ 的梯度相同,其本质上是一个等效梯度。但是其收敛得到的 policy 与 target optimal policy 不同
接下来,我们来分析一下 $\rho k_1, \mathrm{sg}(\rho)k_2, \rho k_3$ 这三种估计的梯度的 variance, 为了避免混淆,【2】使用了 “projection variance in any direction” 的概念,即任意取一个向量 $u$, 然后计算 $\rho k_1$ 和后两者之间对应的 variance 的差(由于 $\mathrm{sg}(\rho)k_2$ 的梯度与 $\rho k_3$ 相同,因此这里我们仅计算 $\rho k_3$),得到:
$$ \begin{aligned} \mathrm{var}[\nabla_\theta (\rho k_1)^Tu] - \mathrm{var}[\nabla_\theta (\rho k_3)^Tu] &= (\mathbb{E}_{\pi_{old}}[(\nabla_\theta (\rho k_1)^Tu)^2] -\mathbb{E}_{\pi_{old}}^2[\nabla_\theta (\rho k_1)^Tu] ) - (\mathbb{E}_{\pi_{old}}[(\nabla_\theta (\rho k_3)^Tu)^2] -\mathbb{E}_{\pi_{old}}^2[\nabla_\theta (\rho k_3)^Tu] ) \\ &= \mathbb{E}_{\pi_{old}}[(\nabla_\theta (\rho k_1)^Tu)^2] - \mathbb{E}_{\pi_{old}}[(\nabla_\theta (\rho k_3)^Tu)^2]\\ &= \mathbb{E}_{\pi_{old}}[\rho(x)^2(s(\theta)(x)^Tu)^2(2k_1(x)+1)] \end{aligned} $$当 $\pi_\theta$ 和 $\pi_{ref}$ 比较接近时,我们有
$$ \frac{\pi_{ref}(x)}{\pi_\theta(x)} = 1+\epsilon(x), \text{ where } |\epsilon(x)| << 1 $$此时
$$ 2k_1(x) + 1 = 1-2\log(1+\epsilon(x))\approx 1-2\epsilon(x) \geq 0 $$从而我们有
$$ \boxed{\mathrm{var}[\nabla_\theta (\rho k_1)]\geq \mathrm{var}[\nabla_\theta (\rho k_3)]=\mathrm{var}[\nabla_\theta (\mathrm{sg}(\rho)k_2)]} $$即当 $\pi_\theta$ 和 $\pi_{ref}$ 比较接近时,$\rho k_3$ 的 variance 比 $\rho k_1$ 更小,这是由于 $\rho s_\theta (k_1+1)$ 额外包含了一个 期望为零的项,这导致了其 variance 比较高。在 DeepSeek-V3.2 中,作者就使用了 $\rho k_3$ 来降低梯度的 variance, 提高训练的稳定性。
【3】将相关的估计总结为了下表的形式
| Type | Loss | Gradient | Expected gradient | Objective | Biased | Variance |
|---|---|---|---|---|---|---|
| on/off-policy | $\rho k_1$ | $\rho s_\theta (k_1+1)$ | $\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})$ | reverse KL | unbiased | high |
| on/off-policy | $\rho k_2$ | $\rho s_\theta (k_1+k_2)$ | $\nabla_\theta\mathbb{E}_{\pi_{\theta}}[k_2]$ | f-divergence | biased | - |
| on/off-policy | $\mathrm{sg}(\rho) k_2$ | $\rho s_\theta k_1$ | $\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})$ | reverse KL | unbiased | low |
| on/off-policy | $\rho k_3$ | $\rho s_\theta k_1$ | $\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})$ | reverse KL | unbiased | low |
【3】还强调了一点就是我们的损失函数必须显式包含 $\rho$, 在 on-policy 场景下,虽然 $\rho\equiv1$, 但是在反向传播时我们通过 $\nabla_\theta \rho=s_\theta$ 保留了采样信息从而避免了梯度估计期望的错配问题。
对于 $\rho k_1$ variance 比较高的特点,我们还可以采用 variance reduction 的方法来降低不同估计的 variance. 【TODO】
analytic gradient 当 action space 有限时,我们还可以使用解析梯度【TODO】
As a Reward Reshaping Item
接下来我们来探究一下第二种形式,即 KL divergence 只影响最终的 reward, 而不参与反向传播。对应的代理目标函数形式为
$$ \mathcal{J}_3(\theta) = \mathbb{E}_{\tau\sim \pi_\theta}\left[R\right] - \beta\ \mathrm{sg}(k_i(\pi_\theta, \pi_{ref})) $$这里 $R=\sum_{t=0}^T\gamma^tr(s_t,a_t)$ 为 accumulative reward
首先,基于前面分析,我们可以得到原始目标函数的梯度为
$$ \begin{aligned} \nabla_\theta \mathcal{J}(\theta) &= \nabla_\theta\mathbb{E}_{\pi_\theta}\left[R\right] - \beta \nabla_\theta D_{KL}(\pi_\theta, \pi_{ref})\\ &= \mathbb{E}_{\pi_\theta}\left[s_\theta R\right]-\beta \mathbb{E}_{\pi_\theta}\left[s_\theta\log \frac{\pi_\theta}{\pi_{ref}}\right]\\ &= \mathbb{E}_{\pi_\theta}\left[s_\theta(R-\beta k_1) \right] \end{aligned} $$代理目标函数的梯度为
$$ \nabla_\theta \mathcal{J}_3(\theta) = \mathbb{E}_{\pi_\theta}\left[s_\theta(R-\beta k_i) \right] $$显然,当我们使用 $k_1$ 时,我们有 $\nabla_\theta \mathcal{J}(\theta)=\nabla_\theta \mathcal{J}_3(\theta)$.
当我们使用 $k_2$ 时,带入 $k_2$ 表达式易知 $\nabla_\theta \mathcal{J}_3(\theta)\neq \nabla_\theta \mathcal{J}(\theta)$,
当我们使用 $k_3$ 时,
$$ \begin{aligned} \mathbb{E}_{\pi_\theta}\left[s_\theta k_i \right] &= \mathbb{E}_{\pi_\theta}\left[s_\theta \left(\frac{\pi_{ref}}{\pi_\theta}-1- \log \frac{\pi_{ref}}{\pi_\theta} \right)\right]\\ &= \mathbb{E}_{\pi_\theta}\left[s_\theta \frac{\pi_{ref}}{\pi_\theta}\right] - \mathbb{E}_{\pi_\theta}\left[s_\theta \right] - \mathbb{E}_{\pi_\theta}\left[s_\theta \log \frac{\pi_{ref}}{\pi_\theta} \right]\\ &=s_\theta k_1 -\nabla_\theta D_{KL}(\pi_{ref}\parallel \pi_\theta) \end{aligned} $$此时,$\nabla_\theta \mathcal{J}_3(\theta)\neq \nabla_\theta \mathcal{J}(\theta)$. 因此,在 on-policy 场景下,只有 $k_1$ 对应的梯度是无偏的
在 off-policy 场景下,由于 Off-policy 只影响 $R$ 的计算,因此原始目标函数和代理目标函数的梯度仍然保持不变,on-policy 场景的结论也适用。
总之,当我们将 KL divergence 作为 reward reshaping item 时,只有 $k_1$ 产生的梯度是无偏的。
Comparison of Two Paradigms
接下来我们来比较一下 KL divergence 作为 loss 和 reward shaping item 的异同之处。首先,两者对于梯度的贡献分别为
$$ \begin{align} &\rho s_\theta k_1\tag{loss}\\ & \mathbb{E}_{\pi_{old}}[\rho s_\theta k_1]\tag{reward shaping} \end{align} $$即两者在期望上时一致的。但是两者也存在不一致的地方,即 KL divergence 作为 loss 时不会影响 $R$, 而作为 reward shaping item 时会影响。因此这就导致两者的优化方向不一致。
Experiments
首先,我们来验证前面的结论,我们构造一个包含 $100$ 个 arms 的 multi-arm bandits, 然后令
$$ \pi_{ref}=\epsilon_1, \pi= \epsilon_1+\epsilon_2 $$其中 $\epsilon_1,\epsilon_2\sim\mathcal{N}(0,1)$, 我们实验 100 次然后取平均值,然后分别计算 estimator 与真实 KL divergence 之间的 MSE 和 estimator gradient 与真实 kl divergence gradient 的 RMSE, 结果如下图所示
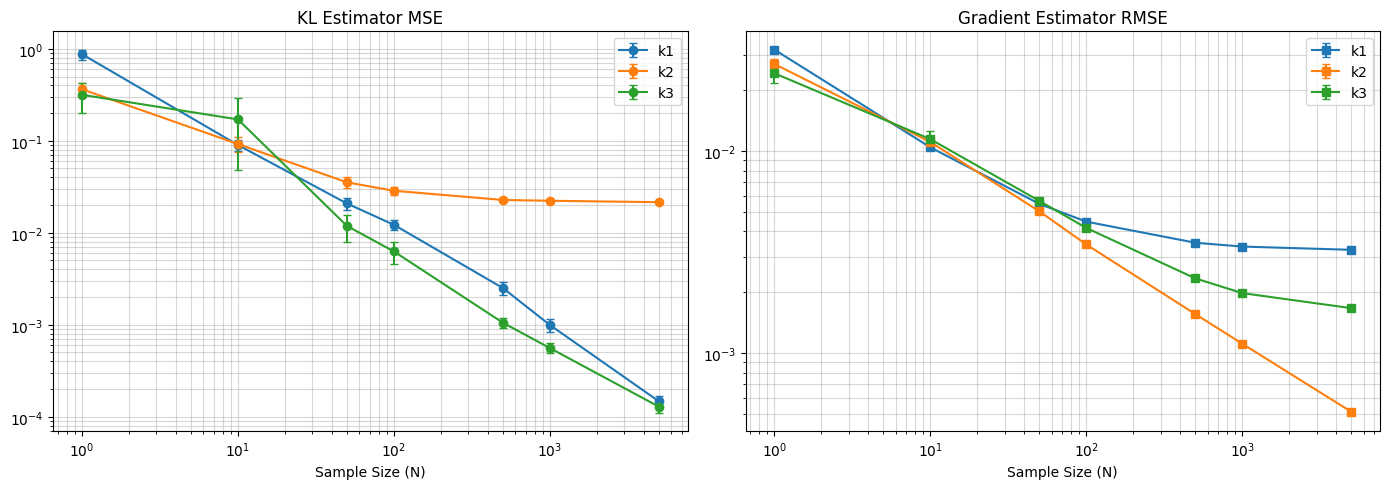
可以看到,这验证了我们之前分析的结论,即 $k_1$ 和 $k_3$ 是无偏估计,而在计算梯度时,只有 $k_2$ 梯度的期望与真实 KL divergence 的梯度相同。
Overview
我们在本节总结前面的分析,如下表所示
| Type | Loss | Gradient | Expected gradient | Objective | Biased | Variance |
|---|---|---|---|---|---|---|
| on-policy | $k_1$ | $s_\theta$ | $0$ | constants | biased | - |
| on-policy | $k_2$ | $-\log r s_\theta$ | $\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})$ | reverse KL | unbiased | |
| on-policy | $k_3$ | $(1-r)s_\theta$ | $\nabla_\theta D_{KL}(\pi_{ref}\parallel \pi_\theta)$ | forward KL | biased | - |
| on/off-policy | $\rho k_1$ | $\rho s_\theta (k_1+1)$ | $\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})$ | reverse KL | unbiased | high |
| on/off-policy | $\rho k_2$ | $\rho s_\theta (k_1+k_2)$ | $\nabla_\theta\mathbb{E}_{\pi_{\theta}}[k_2]$ | f-divergence | biased | - |
| on/off-policy | $\mathrm{sg}(\rho) k_2$ | $\rho s_\theta k_1$ | $\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})$ | reverse KL | unbiased | low |
| on/off-policy | $\rho k_3$ | $\rho s_\theta k_1$ | $\nabla_\theta D_{KL}(\pi_\theta\parallel \pi_{ref})$ | reverse KL | unbiased | low |
| on/off-policy | $\rho\mathrm{sg}(k_1)$ | - | - | - | unbiased | - |
| on/off-policy | $\rho \mathrm{sg}(k_2)$ | - | - | - | biased | - |
| on/off-policy | $\rho \mathrm{sg}(k_3)$ | - | - | - | biased | - |
Conclusion
在本文中,我们详细介绍了 KL-divergence 的基本性质,相关估计方法以及在机器学习特别是 RL 领域中的应用。最终结论为:
- 如果希望稳定可控,则将 KL divergence 作为 loss item; 如果希望更灵活,与奖励信号结合的话,则将其作为 reward shaping item.
- 使用 KL divergence 作为 loss item 时,on-policy 场景下使用 $k_2$ 近似 KL divergence 效果最好;off-policy 场景下,使用 $\mathrm{sg}(\rho)k_2, \rho k_3$ 效果最好
- 使用 KL divergence 作为 reward shaping item 时,$k_1$ 的效果最好