Introduction
目前已经有了针对 dense LLM 的 scaling law, 如 Kaplan scaling law 和 Chinchilla scaling law.
但是,对于 MoE 模型,目前还缺乏一个比较系统的 scaling law.
为了解决这个问题,作者提出了 efficiency leverage (EL), 用于衡量 MoE 模型的效率,其定义为
$$ EL(\mathcal{X}_{\mathrm{MoE}}\mid \mathrm{Dense})=\frac{C_{\mathrm{Dense}}}{C_{{\mathrm{MoE}}}} $$其中 $C_{\mathrm{Dense}}, C_{{\mathrm{MoE}}}$ 分别代表了训练模型所需要的算力。EL 衡量了 moe 模型达到对应 dense 模型表现所需要的算力,EL 值越大,说明 MoE 模型效率越高。EL 的可视化如下图所示
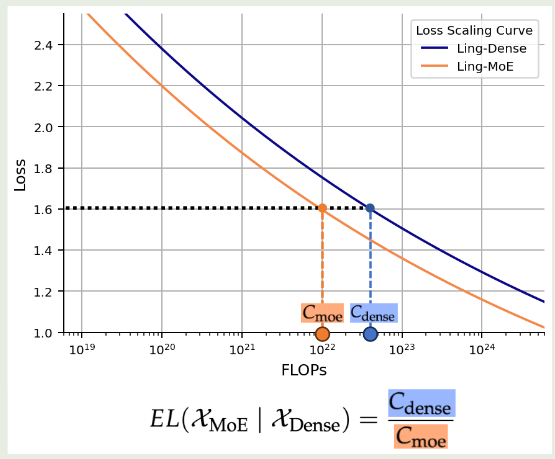
作者通过训练多个模型,探究了 MoE 架构与 EL 之间的关系。作者发现,MoE 模型的表现主要与专家激活比例以及算力相关。基于 scaling law, 作者训练了 Ling-mini-beta, 一个 17.5B-A0.85B 的 MoE 模型,其表现超过了 6.1B dense 模型的表现。
Preliminary
| Notation | description |
|---|---|
| $N$ | total parameters |
| $N_a$ | active parameters |
| $E$ | routed experts |
| $E_a$ | activated experts |
| $E_s$ | shared experts |
作者定义 activation ratio 如下:
$$ A = \frac{E_a+E_s}{E+E_s} $$定义 sharing ratio 如下
$$ S=\frac{E_s}{E_a+E_s} $$定义 expert granularity 如下
$$ G = \frac{d_{\mathrm{model}}}{d_{\mathrm{Expert}}} $$与 DeepSeek-LLM 一样,作者使用 $C=MD$ 来表示算力,non-embedding FLOPs $M$ 和训练 token 数 $D$ 之间的关系。
Hyper Parameters
作者首先探究了针对 MoE 模型的超参数配置,最终你和出来的结果如下图
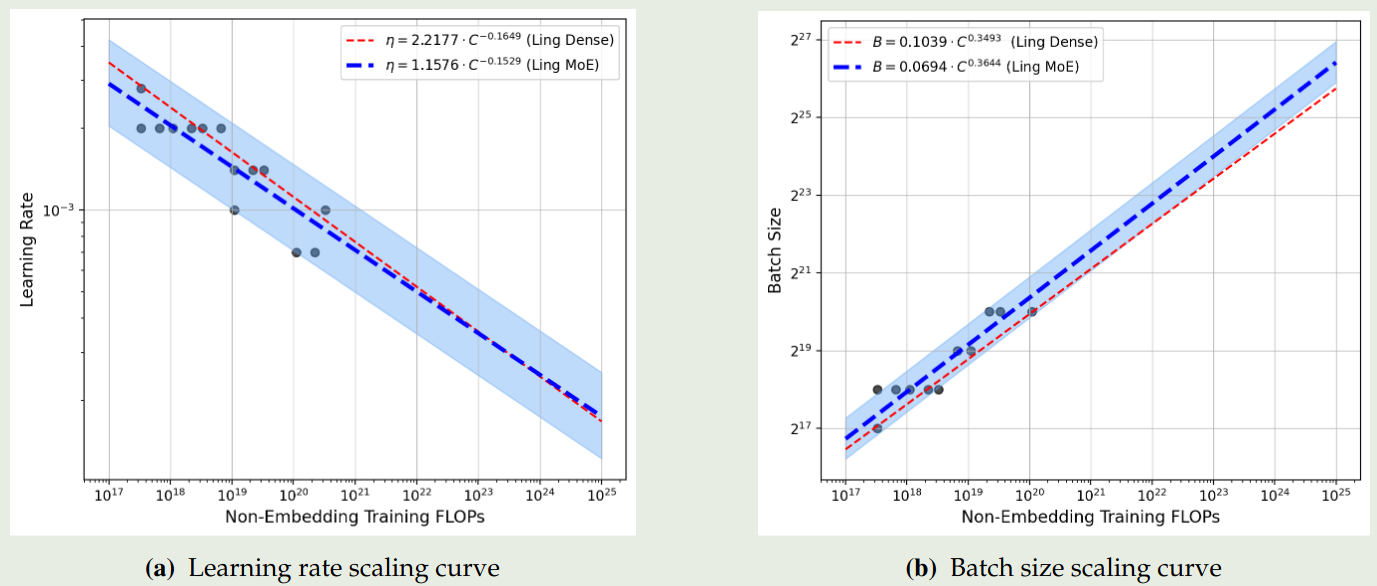
实验结果说明,相比于 dense model, MoE model 需要更大的 batch size.
作者基于这个 scaling law 进行了验证,结果说明这个 scaling law 比较准确。
Parameters and Dataset Size
接下来作者探究了对于模型参数量以及训练 token 个数之间的 scaling law, 求解的问题如下
$$ (M^{opt}, D^{opt}) = \arg\min_{M,D}\mathcal{L}(M,D;C,A,G,S)\quad s.t.\ C=MD $$实验结果如下图所示
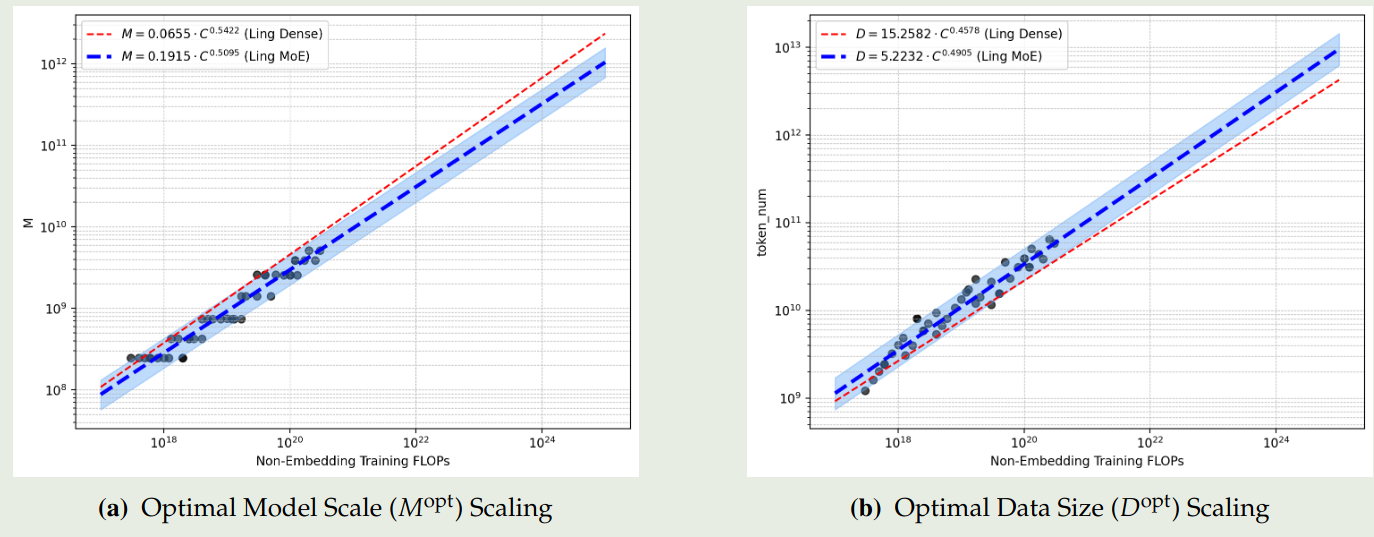
结果说明,不同架构对应的系数接近 $0.5$, 说明我们应该将算力均衡分配到数据和 model size 上。领一方面,MoE 模型可以通过使用更多的数据来达到更优的表现。
Efficiency Leverage
作者将 Efficiency Leverage (EL) 定义为给定算力 $C_{target}$ 和一个 MoE 模型 $\mathcal{X}_{MoE}$, 对应 dense 模型达到 $\mathcal{X}_{MoE}$ 相同的表现所需要的算力 $C_{dense}$, 即
$$ \begin{aligned} &EL(\mathcal{X}_{\mathrm{MoE}}\mid \mathrm{Dense};C_{target})=\frac{C_{\mathrm{Dense}}}{C_{{\mathrm{MoE}}}}\\ s.t.\ & |\mathcal{L}(C_{MoE}, \mathcal{X}_{\mathrm{MoE}})-\mathcal{L}(C_{dense}, \mathcal{X}_{\mathrm{dense}})|\leq \epsilon (\epsilon\to 0) \end{aligned} $$EL 值越高说明 MoE 模型越有效。为了公平起见,dense 模型和 MoE 模型的架构参数基本相同,作者只改变 $d_{model}, d_{ffn}, d_{expert}$ 以及 $n_{layer}$.
接下来,作者就探究了给定算力的情况下,最优的 MoE 配置,即
$$ (A^{opt}, G^{opt}, S^{opt}) = \arg\min_{(A,G,S)\in\mathcal{X}_{\mathrm{MoE}}}EL(\mathcal{X}_{\mathrm{MoE}}\mid \mathrm{Dense};C) $$Scaling Law
首先,坐着探究了最优的 activation ratio $A$, 即
$$ A^{opt} = \arg\min_{A}\mathcal{L}(A;C,M,G,S) $$拟合的结果如下图所示
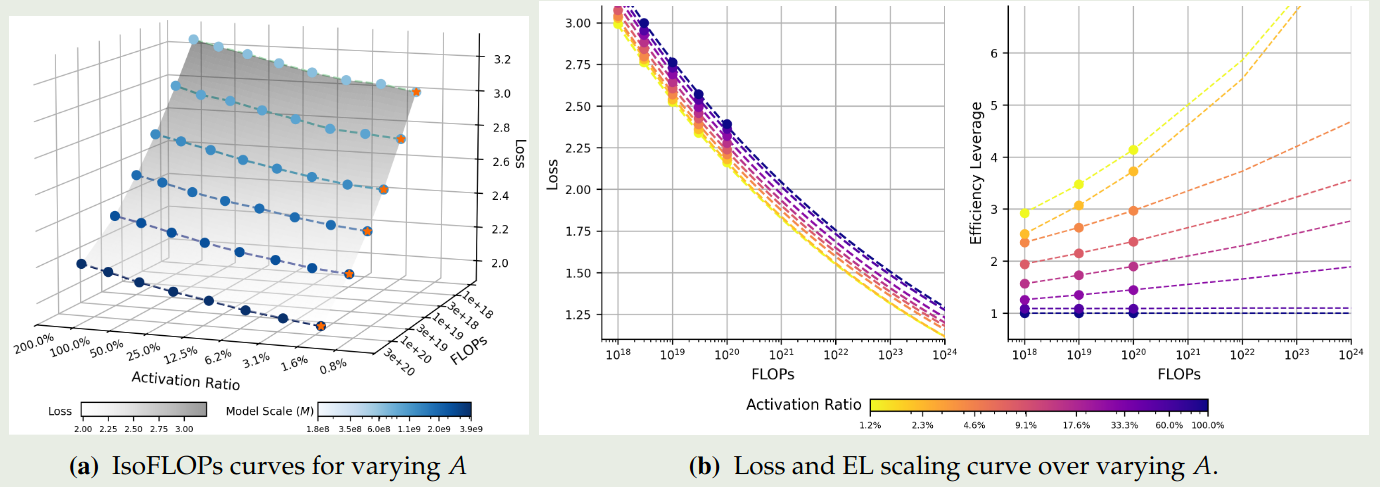
实验结果表明:
- 模型表现随激活比例降低 er 提高
- 更系数的模型对于算力的提升其效率也提升更快
然后,作者探究了最优的 granularity ratio, 即
$$ G^{opt} = \arg\min_{G}\mathcal{L}(G;C,M,A,S) $$拟合的结果如下图所示
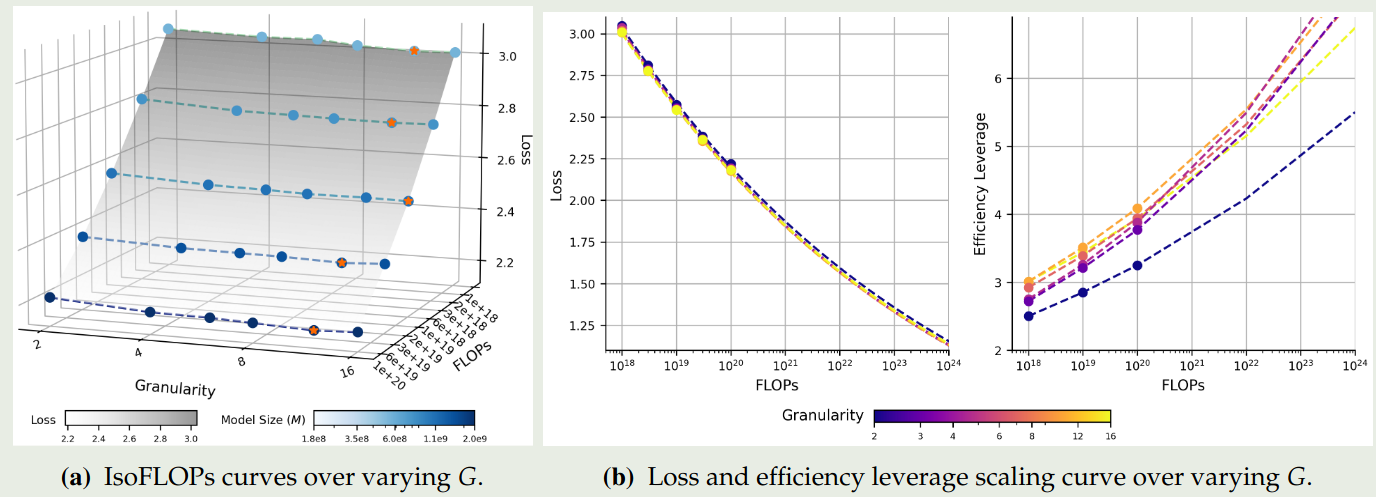
可以看到,无限制提升 granularity 并不会提高模型的表现。并且,不同的算力对应的最优 granularity 处于一个固定的范围
接下来,作者探究了最优的 shared expert ratio, 即
$$ S^{opt} = \arg\min_{S}\mathcal{L}(S;C,M,A,G) $$拟合的结果如下图所示
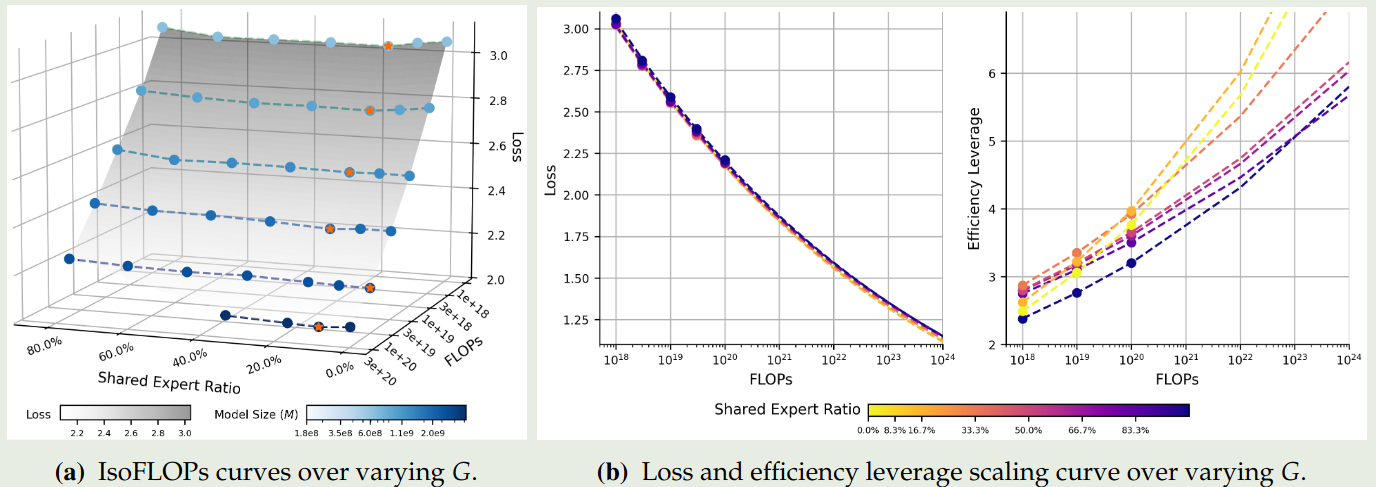
结果说明 shared expert 的比例也不是越多越好,其存在最优值。并且给定算力的情况下,非零最小值的 shared expert 表现最好。因此作者认为,一个 shared expert 的效果最好。
作者还探究了其他可能的因素,结论如下:
- 与 DeepSeek-V3 一样,将 early layer 替换为 dense layer 可以避免 routing imbalance, 并且不会损害模型的表现
- attention 应该占 $30\%\sim40\%$ 左右的算力才能保证模型的表现和效率。进一步提升 attention 的算力占比虽然会提升表现但是会降低推理效率。
通过前面的发现,作者将 shared expert 设置为 1 个,然后探究 EL 与 activation ratio $A$, granularity $G$, FLOPs $C$ 之间的关系。
首先,作者分别假设 $EL$ 与 $A$, $G$, $C$ 之间存在如下关系:
$$ \begin{aligned} \log EL_{C,G}(\hat{A}) &= a_A\log\hat{A}, \text{ where }\frac{1}{\hat{A}}=\frac{1}{A+(1/A_{start}-1/A_{\max})^{-1}}+\frac{1}{A_{\max}}\\ \log EL_{C,A}(\hat{G}) &= a_G+b_G(\log G(\log G+c_G))\\ \log EL_{A,G}(C) &= a_C\log C+c_C \end{aligned} $$拟合的结果如下图所示
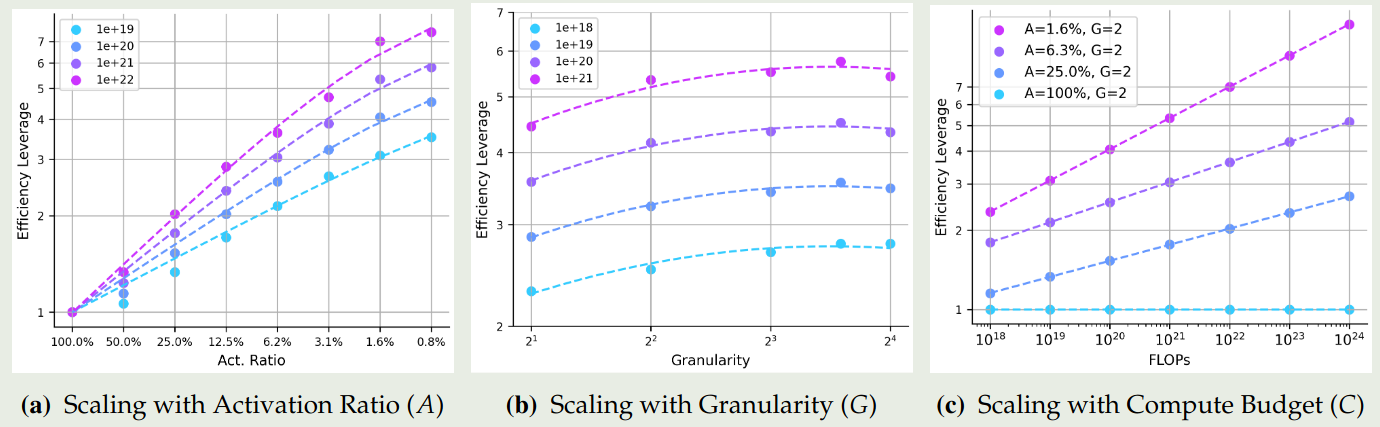
结果显示:
- 提升算力以及降低 activation ratio 都可以提高 EL
- granularity 对 EL 的影响在不同算力的情况下都是一致的
- 对于 MoE 模型,提升算力可以提高 EL
作者的结论为,activation ratio 是影响 MoE EL 的核心因素。并且随着算力的提升,MoE EL 会越来越明显。
作者因此构建了一个统一的公式来统一三个因素
$$ EL(A,G,C) = \hat{A}^{\alpha+\gamma(\log G)^2+\beta \log G} $$其中 $\alpha=a+d\log C$ 代表了 EL 和 activation ratio 之间的关系。拟合出来的参数如下表所示
| $\alpha$ | $d$ | $\gamma$ | $\beta$ | $A_{start}$ | $A_{\max}$ |
|---|---|---|---|---|---|
| 1.23 | -7.61e-2 | 1.67e-2 | -1.17e-1 | 1.63e-2 | 5.28e+16 |
基于这个结果,作者发现在 1e22 FLOPs 的算力下,一个 activation ratio 为 $3.1\%$, granularity 为 $12$ 的 MoE 模型,其 EL 为 $7$.
Ling-mini-beta
基于上一节的发现,作者构建了 Ling-mini-beta, 一个 17.5B 总参数,激活参数为 0.85B 的 MoE 模型。训练使用了 1T token, 模型参数如下表所示
| Model | $n_{\text{layers}}$ | $d_{\text{model}}$ | $d_{\text{ffn}}$ | $d_{\text{expert}}$ | $n_{\text{heads}}$ | $n_{\text{kv\_head}}$ | $E$ | $E_a$ | $E_s$ | $N$ | $N_a$ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Dense 6.1B | 28 | 4096 | 14336 | - | 32 | 8 | - | - | - | 6.11B | 6.11B |
| Ling-mini-beta (A0.8B) | 20 | 2048 | 5120 | 384 | 16 | 4 | 384 | 12 | 1 | 17.5B | 0.85B |
训练的损失变化情况如下图所示
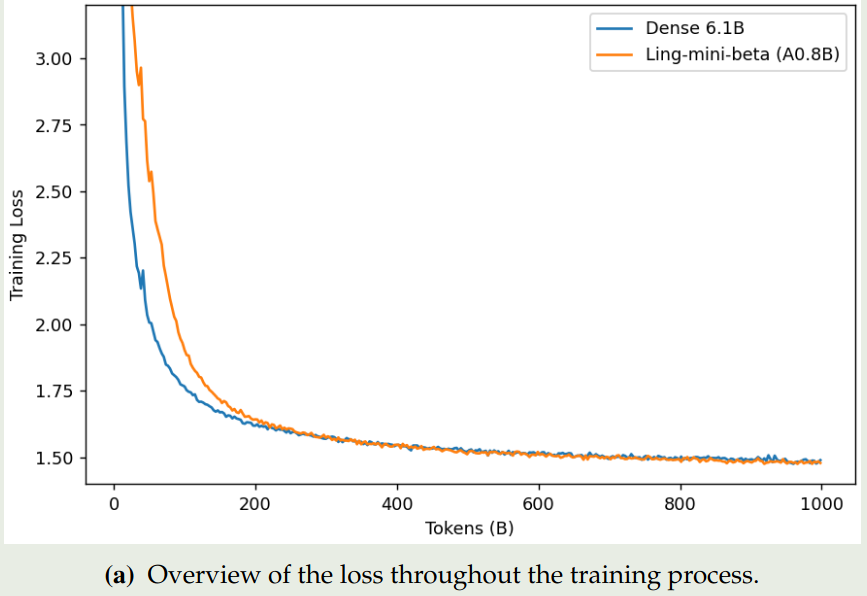
从图中我们可以看出,dense model 一开始的损失下降比较快,但是其最终表现不如 moe 模型。
Conclusion
在本文中,作者提出了 Efficiency Leverage, 一个衡量 MoE 模型相对于 dense 模型计算效率的 metric, 作者构建了针对 MoE 模型的 scaling law. scaling 揭示了两个主要影响 MoE 模型效率的因素:算力与激活参数比例。基于 scaling law, 作者构建了 Ling-mini-beta, 一个 17B-A0.8B 的 MoE 模型,其效率超过了对应 dense 模型的 7 倍。