Introduction
已有的 MoE 模型往往都会使用 load balancing loss 来避免 Imbalanced routing, 但是加入这个额外的损失之后,模型训练的梯度也会受到影响。
DeepSeek 基于这个问题提出了 Loss-Free Balancing, 该方法不引入额外的 loss item, 而是在 routing 的结果上加入一个 bias item, bias item 可以根据 expert load 来动态更新进而实现 load balancing.
Method
MoE definition
$$ \begin{aligned} h_t &= u_t + \sum_{i=1}^Ng_{i,t}\mathrm{FFN}_i(u_t),\\ g_{i,t} &= \begin{cases} s_{i,t}, & s_{i,t}\in\mathrm{Topk}(\{s_{i,j}\mid 1\leq j\leq N\}, K)\\ 0, &\text{otherwise} \end{cases}\\ s_{i,t} &= G(u_t^Te_i), \end{aligned} $$其中 $G$ 是 gating function, $e_i$ 是第 $i$ 个专家对应 gating function 的权重
load balancing loss 有两个作用:
- 避免 routing collapse, 即模型只选择固定的少数专家完成任务
- 减少通信开销
但是引入 load balancing loss 会对 LLM 的训练产生影响,为了避免对模型性能造成影响,我们需要小心设置 load balancing loss 的权重,实验结果如下图所示
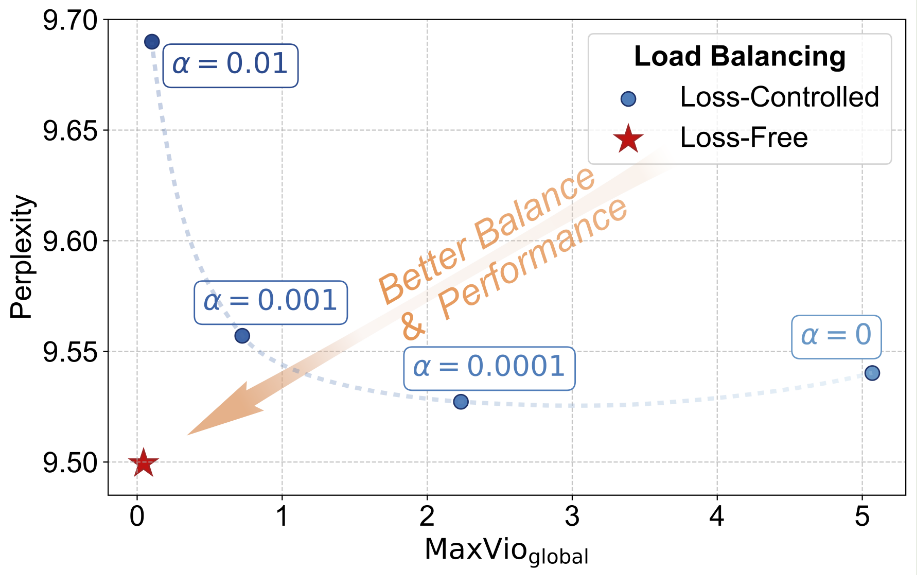
为了解决这个问题,作者提出了 Loss-Free Balancing, 具体做法就是在每个专家的 gating score 上加入一个 bias term, 然后再决定对应的专家:
$$ g_{i,t} = \begin{cases} s_{i,t}, & s_{i,t}+b_i\in\mathrm{Topk}(\{s_{i,j}+b_j\mid 1\leq j\leq N\}, K)\\ 0, &\text{otherwise} \end{cases} $$注意这里的 bias item 仅影响 top-K 操作,其对最终的输出没有影响。
为了实现负载均衡,作者根据上一个 batch 的 expert load 情况来调整 bias item, 如果某一个专家的 load 太大,则对应的 bias item 会变小。 其算法实现过程如下:

作者对比不同的负载均衡算法如下表所示
| Load Balancing Methods | Balanced Expert Load | Interference Gradients | Future Token Leakage |
|---|---|---|---|
| Loss-Controlled (strong auxiliary loss) | balanced | strong | no leakage |
| Loss-Controlled (weak auxiliary loss) | imbalanced | weak | no leakage |
| Expert Choice | balanced | none | with leakage |
| Loss-Free (Ours) | balanced | none | no leakage |
Experiments
作者使用了 DeepSeekMoE 来进行实验,作者使用了 sigmoid function 作为 gating function, 因为作者发现 sigmoid function 效果比 softmax 效果更好。
作者提出了 maximal violation (MaxVio) 来量化一个 MoE layer 的负载均衡程度
$$ \mathrm{MaxVio} = \frac{\max_i\mathrm{Load}_i-\overline{\mathrm{Load}_i}}{\overline{\mathrm{Load}_i}} $$其中 $\mathrm{Load}_i$ 代表了分配给第 $i$ 个专家的 token 个数,$\overline{\mathrm{Load}_i}$ 代表了理想情况下的负载均衡。
实验结果如下图所示
| Model Size | Load Balancing Methods | Validation Perplexity | MaxVioglobal |
|---|---|---|---|
| 1B | Loss-Controlled | 9.56 | 0.72 |
| 1B | Loss-Free | 9.50 | 0.04 |
| 3B | Loss-Controlled | 7.97 | 0.52 |
| 3B | Loss-Free | 7.92 | 0.04 |
实验结果显示,本文提出的 Loss-Free Balancing 效果更好,且负载均衡更高
作者还展示了训练过程的负载情况如下
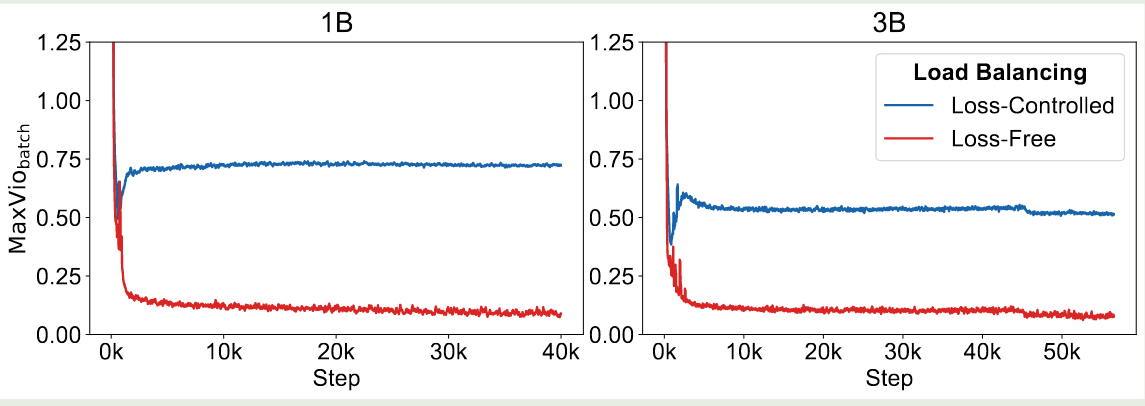
可以看到,Loss-Free 的负载一直比 load balancing loss 效果更好
Ablation Study
作者首先探究了 bias term 更新速率对模型表现的影响,结果如下图所示
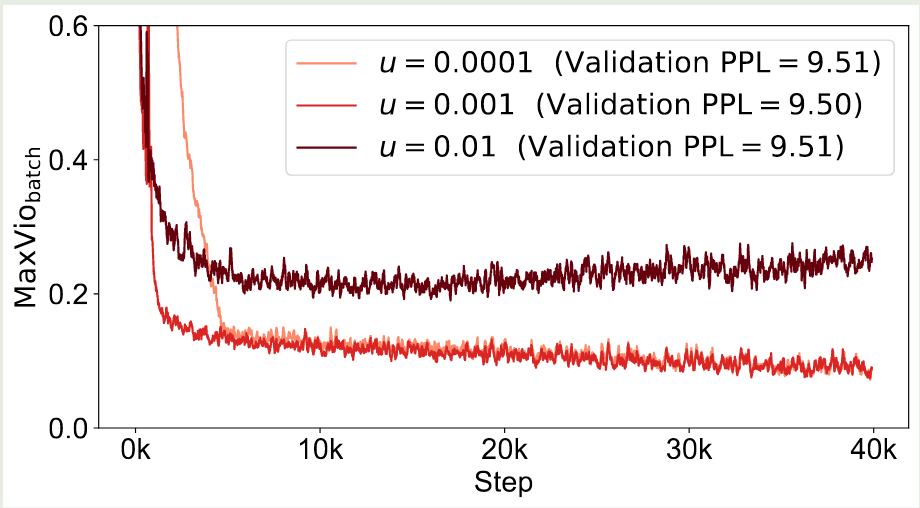
结果显示,使用过大的 update rate 会影响最终的负载均衡,而较小的 update rate 收敛速率比较慢。因此作者在本文中使用了 $u=0.001$ 这个设置
作者还对比了 baseline model 使用 softmax 个 sigmoid gating 两种方式,结果如下图所示
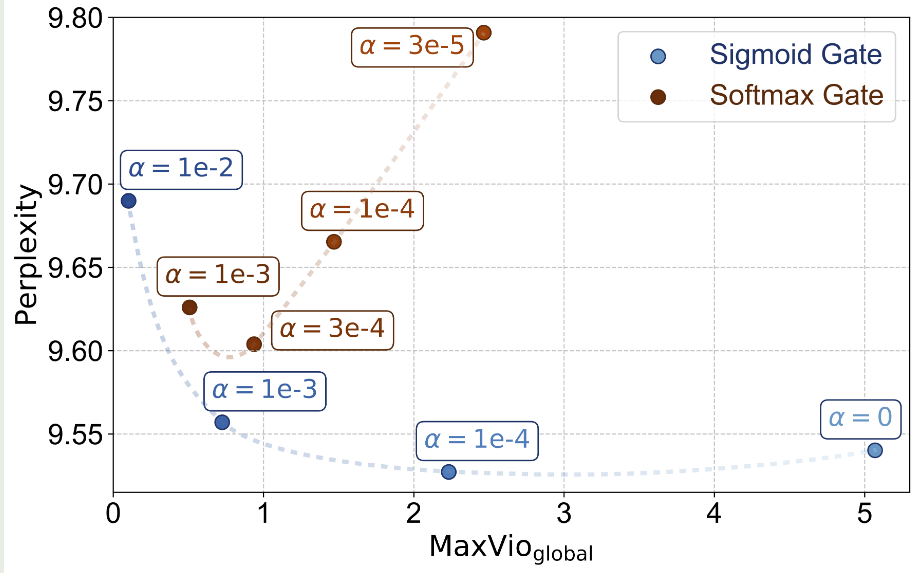
实验结果显示,Sigmoid function 对于超参数更加 robust, 且表现也更好一些。
作者还尝试了不同的 bias 更新方式,结果显示尽管不同的更新方式有可能会提高 load balance, 但是最终模型表现提升不大。
Conclusion
作者在本文中提出了 Loss-Free Balancing 策略,一个针对 MoE 负载均衡而不需要额外损失项的方法