DeepSeek 在 2024 年 5 月提出了 multi-head latent attention (MLA), 用于提高 attention 的 Inference 效率
Introduction
传统的 multi head attention (MHA) 虽然效果好,但是在 inference 时,其 KV cache 会变成瓶颈,影响推理效率。为了解决这个问题,已有的工作如 MQA 和 GQA 通过共享权重来减少 KV cache 内存占用,但是结果发现模型的表现也会降低。
为了解决这个问题,作者提出了 multi-head latent attention (MLA), 来压缩 KV cache.
Related Work
MHA
令 $d$ 为 hidden size, $n_h$ 为 attention heads 的个数,$\ell$ 为 transformer layer 的层数,$d_h$ 为每个 head 的 dimension, $h_t\in\mathbb{R}^d$ 为 attention layer 中第 $t$ 个 token 对应的 hidden states。对于标准的 MHA, 我们首先计算 Q, K, V 如下:
$$ q_t=W^{Q}h_t,\quad k_t=W^Kh_t,\quad v_t = W^Vh_t $$其中,$W^Q,W^K,W^V\in\mathbb{R}^{d_hn_h\times d}$ 分别为 query, key, value projection layer 的权重。接下来 MHA 的计算方式如下
$$ \begin{aligned} o_{t,i} &= \sum_{j=1}^t\mathrm{softmax}_j\left(\frac{q_{t,i}^Tk_{j,i}}{\sqrt{d_h}}\right)v_{j,i},\\ u_t&= W^O[o_{t,1};o_{t,2};\dots,;o_{t,n_h}] \end{aligned} $$其中 $q_t=[q_{t,1};q_{t,2};\dots,;q_{t,n_h}]$, $k_t=[k_{t,1};k_{t,2};\dots,;k_{t,n_h}]$, $v_t=[v_{t,1};v_{t,2};\dots,;v_{t,n_h}]$. $W^O\in\mathbb{R}^{d\times d_hn_h}$ 为 output projection 的权重。在 inference 阶段,每个 token 需要缓存其 key 以及 value 对应的值,从而每个 token 的 kv cache 占用为 $2n_hd_h\ell$. 当序列长度过大时,KV cache 会影响整体的 inference efficiency.
MQA & GQA
MQA 通过在所有的 heads 中共享 key 和 value 来实现降低 kv cache 的作用,在 MQA 中,$W^K, W^V\in\mathbb{R}^{d_h\times d}$, 在计算时,对应的 $k_t$ 和 $v_t$ 通过广播机制参与 attention 的计算。此时,KV cache 占用为 MHA 的 $1/n_h$, 即 $2d_h\ell$.
但是,MQA 的问题是表达能力太弱(表现差),因此后续 GQA 进行了改进,GQA 在 MQA 和 MHA 之间进行了权衡,即将 heads 分为若干个 group, 每个 group 中共享 key 和 value, 即 $W^K, W^V\in\mathbb{R}^{n_gd_h\times d}$, 这里 $n_g$ 是 group 个数,在计算 attention 时,key 和 value 在 group 内部共享,此时,GQA 的 KV cache 占用是 MQA 的 $n_g$ 倍,即 $2n_gd_h\ell$.
MLA
MLA 的架构图如下所示
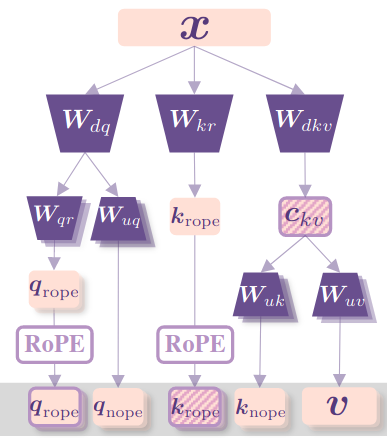
MLA 使用 low-rank joint compression 来压缩 key 以及 value 的 KV cache:
$$ c_t^{KV} = W^{DKV}h_t,\quad k_t^C = W^{UK}c_t^{KV}, v_t^C = W^{UV}c_t^{KV} $$这里 $c_t^{KV}\in\mathbb{R}^{d_c}$ 为 key 以及 value 压缩后的 latent vector. $d_c< 另外,为了减少训练时的 activation memory, 作者对于 query 同样也执行了 low-rank compression, 压缩方式如下 其中 $c_t^Q\in\mathbb{R}^{d_c'}$ 为 query 压缩后的 latent vector, $d_c'<< d_hn_h$ 为 query compression dimension, $W^{DQ}\in\mathbb{R}^{d_c'\times d}$, $W^{UQ}\in\mathbb{R}^{d_hn_h\times d_c'}$ 分别时 down projection, up projection matrix. 最后 attention 的计算与 MHA 保持一致: 在推理的时候,我们只需要缓存 $c_t^{KV}$ 即可,这样每个 token 的 KV cache 为 $d_c\ell$. 并且在 inference 时,我们可以将 $W^{UK}$ 和 $W^{Q}$ 融合在一起,将 $W^{UV}$ 和 $W^{O}$ 融合在一起,也就是说我们不需要显式的计算出 $k_t$ 以及 $v_t$, 即 以及 这里 $W^O = [W^O_1,\dots,W^O_{n_h}]$, $W^{UV}=[W^{KV}_1;\dots;W^{KV}_{n_h}]$, $W_i^O\in\mathbb{R}^{d\times d_h}$, $W^{UV}_i\in\mathbb{R}^{d_h\times d_c}$. 接下来,作者介绍了如何解决 RoPE 不相容的问题。如果说我们直接在 $k_t^C$ 上进行 RoPE, 那么我们有 此时,我们没有办法将 $W^{UK}$ 吸收到 $W^{UQ}$ 中,这样就导致在 inference 时我们必须重新计算所有 prefix token 对应的 key, 这显然会降低 inference efficiency 为了解决这个问题,作者使用了partial RoPE的技巧,即将query和key拆解为NoPE以及RoPE两部分,前者由MLA产生,后者携带位置信息。RoPE部分包括query $q_{t,i}^R\in\mathbb{R}^{d_h^R}$ 以及一个共享的 key $k_t^R\in\mathbb{R}^{d_h^R}$, 其中 $d_h^R$ 是 decoupled query 以及 decoupled key 的 head dimension. [!remark]
这里 key 对应的 RoPE 共享的原因是这部分信息也需要使用 KV cache 进行缓存,通过共享可以降低 KV cache 占用;而 query 对应的 RoPE 不共享的原因是提高 head 的表达能力,与 MHA 原理一致。 对应 MLA 的计算公式如下 其中 $q_t^R=[q_{t,1}^R;q_{t,2}^R;\dots,;q_{t,n_h}^R]$, $W^{QR}\in\mathbb{R}^{d_h^Rn_h\times d_c'}$, $W^{KR}\in\mathbb{R}^{d_h^R\times d}$ . $\mathrm{RoPE}(\cdot)$ 只执行 RoPE 矩阵乘法的操作。 在这种情形下,attention 的计算如下所示 可以看到,现在 attention 的计算分为了两部分,一部分是 MLA 自身的计算,这部分计算前面已经证明可以通过矩阵吸收的方式来进行优化,第二部分是关于 RoPE 部分的计算,这部分计算量不是很大 最终,MLA 完整的计算公式如下 在 inference 时,decoupled key 也需要被缓存,因此 DeepSeek-V2 每个 token 所需要的 KV cache 为 $(d_c+d_h^R)\ell$, 框选的部分即为 Inference 阶段需要缓存的内容 MLA 与 MHA, MQA, GQA 的对比如下图所示 接下来,作者对比了不同 attention 机制的 KV cache, 结果如下表所示 这里作者将 $d_c$ 设置为 $4d_h$, $d_h^R$ 设置为 $d_h/2$, 因此得到了上面的 $9/2d_h\ell$ 的近似。与 GQA 相比,相当于 MLA 使用了 2.25 个 group, 但是可以得到更强的效果。 为了避免 low-rank compression 以及 fine-grained expert segmentation 对输出的 scale 产生影响,作者对 compressed latent vectors $c_t^Q, c_t^{KV}$ 进行了 normalization. 首先是代码变量与公式变量的对应关系 在具体实现时,作者对计算过程进行了优化,具体就是先合并计算然后通过 代码如下所示 首先,我们结合 DeepSeek-V2 的 我们接下来对比一下各个模型架构之间 attention 部分的参数量,可以看到与 MHA 一致,大部分参数量都集中在最后的 Output projection layer 上 作者首先对比了 MHA, GQA, MQA 的表现,作者基于一个 7B 的 dense 模型,使用 1.33T token 进行训练,实验结果如下 实验结果显示,MHA 的表现显著优于 GQA 和 MQA. 这说明了 MQA 和 GQA 虽然减少了 KV cache 的占用,但是相应地,它们对应的表现也有所降低。 接下来,作者对比了 MLA 和 MHA 的表现,实验结果如下 可以看到,MLA 的表现比 MHA 的表现更好,并且 KV cache 也更少。 作者提出了 MLA, 一个基于 low rank compression 的注意力机制,通过将 key value vector 压缩到低维空间,MLA 可以有效降低 Inference latency, 作者通过实现证明 MLA 的表现可以与 MHA 相比,并且 KV cache 更小。Decoupled Position Embedding
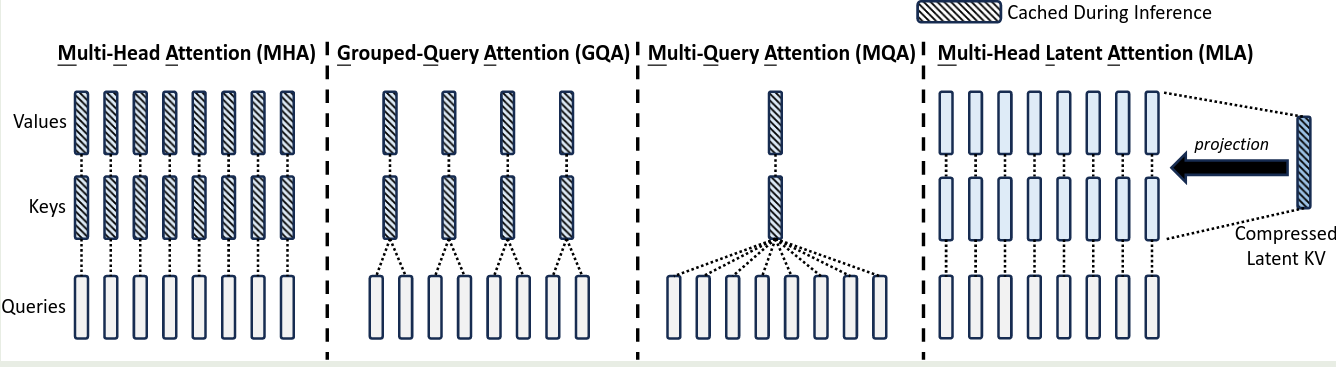
Comparison of KV Cache
Attention Mechanism KV Cache per Token (# Element) Capability Multi-Head Attention (MHA) $2n_hd_h\ell$ Strong Grouped-Query Attention (GQA) $2n_gd_h\ell$ Moderate Multi-Query Attention (MQA) $2d_h\ell$ Weak MLA (Ours) $(d_c+d_h^R)\ell\approx 9/2d_h\ell$ Stronger Code
code name variable name Value hidden_size$d$ 5120 kv_lora_rank$d_c$ 512 q_lora_rank$d_c'$ 1536 qk_nope_head_dim$d_h$ 128 qk_rope_head_dim$d_h^R$ 64 v_head_dim$d_h$ 128 num_attention_heads$n_h$ 128 split 进行拆分,这部分策略应用于三个部分: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class DeepseekV2Attention(nn.Module):
def __init__(self, config, layer_idx):
# d_h + d_h^R
self.q_head_dim = config.qk_nope_head_dim + config.qk_rope_head_dim
# W^{DQ}
self.q_a_proj = nn.Linear(
self.hidden_size, config.q_lora_rank, bias=config.attention_bias
)
# [W^{UQ}; W^{QR}]
self.q_b_proj = nn.Linear(
config.q_lora_rank, self.num_heads * self.q_head_dim, bias=False)
# [W^{DKV}; W^{KR}]
self.kv_a_proj_with_mqa = nn.Linear(self.hidden_size, config.kv_lora_rank + config.qk_rope_head_dim, bias=config.attention_bias)
# [W^{UK}; W^{UV}]
self.kv_b_proj = nn.Linear(config.kv_lora_rank, self.num_heads * (self.q_head_dim - self.qk_rope_head_dim + self.v_head_dim), bias=False)
# W^O
self.o_proj = nn.Linear(self.num_heads * self.v_head_dim, self.hidden_size, bias=config.attention_bias)
def forward(self, hidden_states, ...):
# [q_t^c; q_t^R]
q = self.q_b_proj(self.q_a_layernorm(self.q_a_proj(hidden_states)))
q = q.view(bsz, q_len, self.num_heads, self.q_head_dim).transpose(1, 2)
q_nope, q_pe = torch.split(q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1)
# [c_t^{KV}; k_t^R]
compressed_kv = self.kv_a_proj_with_mqa(hidden_states)
compressed_kv, k_pe = torch.split(compressed_kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1)
k_pe = k_pe.view(bsz, q_len, 1, self.qk_rope_head_dim).transpose(1, 2)
# [k_t^c; v_t^c]
kv = (self.kv_b_proj(self.kv_a_layernorm(compressed_kv)).view(bsz, q_len, self.num_heads, self.qk_nope_head_dim + self.v_head_dim).transpose(1, 2))
k_nope, value_states = torch.split(kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1)
# q_t^R, k_t^R
q_pe, k_pe = apply_rotary_pos_emb(q_pe, k_pe, cos, sin, position_ids)
# q_{t, i}
query_states = k_pe.new_empty(bsz, self.num_heads, q_len, self.q_head_dim)
query_states[:, :, :, : self.qk_nope_head_dim] = q_nope
query_states[:, :, :, self.qk_nope_head_dim :] = q_pe
# k_{t, i}
key_states = k_pe.new_empty(bsz, self.num_heads, q_len, self.q_head_dim)
key_states[:, :, :, : self.qk_nope_head_dim] = k_nope
key_states[:, :, :, self.qk_nope_head_dim :] = k_pe
# Q^TK
attn_weights = (torch.matmul(query_states, key_states.transpose(2, 3)) * self.softmax_scale)
# softmax(...) in FP32
attn_weights = nn.functional.softmax(attn_weights, dim=-1, dtype=torch.float32).to(query_states.dtype)
# o_{t, i}
attn_output = torch.matmul(attn_weights, value_states)
# u_t
attn_output = self.o_proj(attn_output)
return attn_output, attn_weights, past_key_value
参数量计算
config 计算一下 MLA 部分的参数量:Matrix Parameters values ratio $W^{DKV}$ $dd_c$ 2621440 1.91% $W^{UK}$ $d_hn_hd_c$ 8388608 6.12% $W^{UV}$ $d_hn_hd_c$ 8388608 6.12% $W^{DQ}$ $d_c'd$ 7864320 5.74% $W^{UQ}$ $d_hn_hd_c'$ 25165824 18.37% $W^{KR}$ $d_h^Rd$ 327680 0.24% $W^{QR}$ $d_h^Rd$ 327680 0.24% $W^{O}$ $dd_hn_h$ 83886080 61.24% Total $d(d_c+d_c'+2h_h^R)+d_hn_h(2d_c+d_c'+d)$ 136970240 100% Experiments
Benchmark (Metric) # Shots MQA GQA(8 Groups) MHA # Params - 7.1B 6.9B 6.9B BBH (EM) 3-shot 33.2 35.6 37.0 MMLU (Acc.) 5-shot 37.9 41.2 45.2 C-Eval (Acc.) 5-shot 30.0 37.7 42.9 CMMLU (Acc.) 5-shot 34.6 38.4 43.5 Benchmark (Metric) # Shots MHA MLA MHA MLA # Activated Params - 2.5B 2.4B 25.0B 21.5B # Total Params - 15.8B 15.7B 250.8B 247.4B KV Cache per Token (# Element) - 110.6K 15.6K 860.2K 34.6K BBH (EM) 3-shot 37.9 39.0 46.6 50.7 MMLU (Acc.) 5-shot 48.7 50.0 57.5 59.0 C-Eval (Acc.) 5-shot 51.6 50.9 57.9 59.2 CMMLU (Acc.) 5-shot 52.3 53.4 60.7 62.5 Conclusion
References