Notes on Moonlight

Kimi 提出了 Moonlight, 一个基于 Muon optimizer 训练得到的 16B-A3B MoE LLM. 作者详细介绍了如何 scale up muon optimizer.

Introduction

Muon 验证了 Muon optimizer 在小语言模型 nanoGPT 上的表现，但是对于更大规模 LLM 的表现，尚未有人探究。因此 Kimi 就希望在大规模 LLM 上验证 Muon optimizer 的表现。作者主要进行了两点改进：

加入 weight decay
调整了不同参数更新的 scale

基于改进后的 Muon optimizer, 其训练效率相比于 AdamW 提升了 2 倍。作者基于 Muon Optimizer 训练得到了 Moonlight, 一个 16B-A3B 的 MoE LLM.

作者主要作出了三点贡献：

探究了 weight decay 在 scaling Muon 时的作用
分布式 Muon optimizer 的实现
验证了 Muon optimizer 的 scaling law

Method

Background

作者首先介绍了一下 Muon optimizer, 给定步数 $t$, 参数矩阵 $W_{t-1}$, momentum $\mu$, 学习率 $\eta_t$ 以及目标函数 $\mathcal{L}_t$, Muon optimizer 的更新方式如下：

$$ \begin{aligned} M_t &= \mu M_{t-1} + \nabla\mathcal{L}_t(W_{t-1})\\ O_t &= \mathrm{Newton-Schulz}(M_t)\\ W_t &= W_{t-1} - \eta_t O_t \end{aligned} $$

这里 $M_t$ 是 gradient 的 momentum, 初始化为 $M_0=0$. 在上面的更新公式中，Newton-Schulz 的作用是求解 $(M_tM_t^T)^{-1/2}M_t$. 令 $M_t=U\Sigma V^T$ 为 SVD 分解，我们有

$$ (M_tM_t^T)^{-1/2}M_t = UV^T $$

这是一个半正交矩阵，即 $(UV^T)^T(UV^T)=I$.

Newton-Schulz 迭代的具体公式如下：

$$ X_0 = \frac{M_t}{\|M_t\|_F},\quad X_k = aX_{k-1} + b(X_{k-1}X_{k-1}^T)X_{k-1} + c(X_{k-1}X_{k-1}^T)^2X_{k-1} $$

其中，normalization 是为了保证 Newton-Schulz 的收敛性。 $a,b,c$ 是三个超参数，在 Muon 中设置为 $(a,b,c)=(3.4445, 4.7750, 2.0315)$.

Scaling up Muon

作者发现，尽管 Muon 在小规模场景下 work 的很好，但是大规模性场景下的收益就非常有限了。作者发现，这是因为模型的参数以及每一层输出的 RMS 变得很大，这可能会影响模型的性能。因此，作者就和 AdamW 一样使用 weight dacay 来避免这个问题，即

$$ W_t =W_{t-1} - \eta_t(O_t + \lambda W_{t-1}) $$

作者通过实验对比了 AdamW, vanilla Muon 和 Muon w/ weigth decay 三者的表现，实验结果如下图所示

实验结果显示，尽管 vanilla Muon 手链最快，但是由于其权重增长很快，因此最后模型的表现不如 AdamW 和 Muon w/ weigth decay.

接下来，作者分析了以下更新矩阵的 Root Mean Square (RMS), 结论是 Muon optimizer 的 RMS 与参数矩阵的形状相关：

Lemma For a full-rank matrix parameter of shape $[A, B]$, its theoretical Muon update RMS is $\sqrt{1/\max(A, B)}$.

证明如下：通过 Newton-Schulz 迭代，我们得到 $O_t=UV^T$, 其中 $M_t=U\Sigma V^T$ 是 SVD 分解，我们有

$$ \mathrm{RMS}(O_t) = \sqrt{\frac{\sum_{i=1}^A\sum_{j=1}^BO_{t,i,j}^2}{AB}}=\sqrt{\frac{r}{AB}} $$

其中, $r=\mathrm{rank}(M_t)$ , 这样就完成了证明。

而 Adam 和 AdamW 的 RMS 都在 $1$ 附近。作者认为 RMS 也会影响模型表现：

当 $\max(A,B)$ 过大时，如 dense MLP matrix, 其更新就会变得很小，限制了模型的表现
当 $\max(A,B)$ 过小时，如 GQA 中的 KV head 或者 DeepSeek-V3 中的 MLA, 更新又会变得很大，导致训练不稳定。

因此，作者就提出了一个 rescaling 的技巧，来消除 Muon optimizer 的影响。

作者通过实验发现，AdamW 的 RMS 通常在 $0.2\sim0.4$ 左右，因此，作者将 Muon optimizer 的更新设置如下

$$ W_t = W_{t-1} - \eta_t(0.2\cdot O_t\cdot \sqrt{\max(A,B)} + \lambda W_{t-1}) $$

基于这个改变， Muon 和 AdamW 可以共享学习率以及 weight decay 参数。

Distributed Muon

ZeRO-1 天然适合 AdamW, 因为 AdamW 都是 element-wise 进行计算的。但是 Muon 则需要梯度矩阵的全部信息。因此，作者就针对 ZeRO-1 进行适配，提出了 Distributed Muon, 分布式版本将优化器的状态进行切分，然后加入了两个额外的操作：

DP gather: 将 ZeRO-1 切分的梯度矩阵 gather 为一个完整的矩阵
Calculate Full Update: 对完整的梯度矩阵执行 Newton-Schulz 迭代

最终，Distributed Muon 的算法如下图所示

Distributed Muon

最后，作者分析了一下 distributed Muon 和 distributed AdamW 的内存和算力占用：

内存开销：Muon 只有一阶矩，而 AdamW 有二阶矩，因此 Muon 的额外内存开销为 AdamW 的一半。
通信开销：对于 ZeRO-1，通信开销来源于三个过程：All-Gather 参数 $P$ 用于前向传播, Reduce-Scatter 梯度 $G$ 用于反向传播, All-Gather 更新后的参数 $P$ 用于下一轮的前向传播。AdamW 不引入额外通信，所以其每个参数的通信量为 $4+4=8$, 分别代表 $G$ 和 $P$ 的通信量。而 Muon 则需要额外的一次通信来得到 full matrix, 因此每个参数通信量为 $4+4+2=10$, 分别代表 $P, G$ 和 full matrix. 也就是说，分布式 Muon 的通信量最高为 AdamW 的 $1.25$ 倍。实际上由于我们使用 multiple DP, 这个比例会更接近于 $1.0$.
latency：Distributed Muon 相比于 AdamW latency 更高，这是因为 Muon 需要进行 DP gather 以及计算 Newton-Schulz 迭代。但实际上，latency 很小，因为 Newton-Schulz 迭代只需要迭代 5 次，并且 optimizer 的 end-to-end latency 相比于 forward-backward 过程是可以忽略的。一些额外的技巧也可以降低 latency.

实际在训练的过程中，作者发现 Distributed Muon 相比于 AdamW 并没有太明显的 latency.

Experiments

Scaling Law of Muon

作者分析了一下 Muon Optimizer 的 scaling law, 实验结果如下图所示

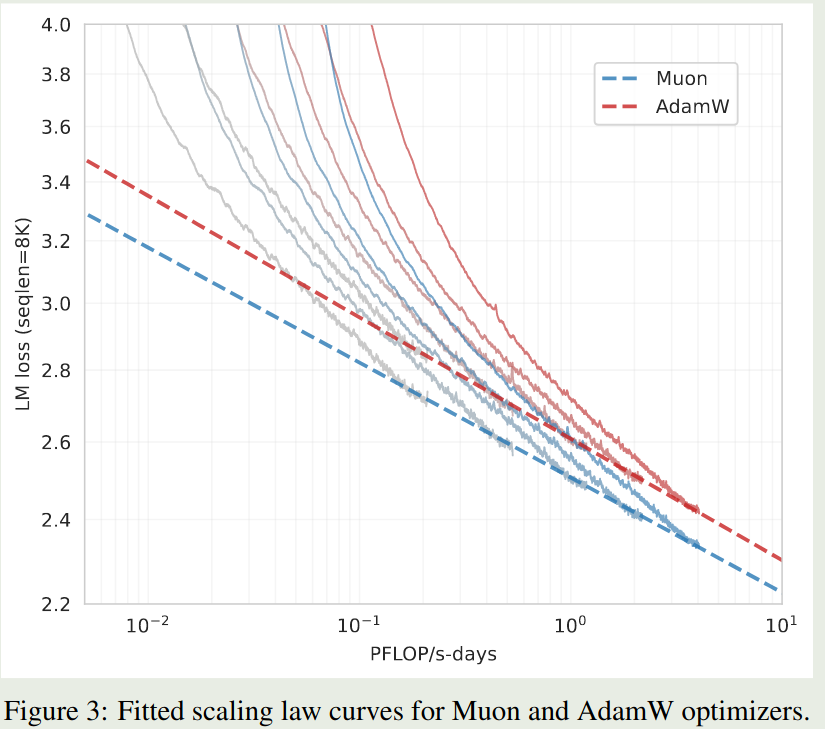
Scaling law for Muon and AdamW

实验结果表明，在最优设置下，Muon Optimizer 只需要 $52%$ 的 FLOPs 就可以达到 AdamW 的表现

Pretraining with Muon

作者分贝使用 AdamW 和 Muon 训练模型，然后评测了以下模型在不同 benchmark 上的表现，结果如下图所示

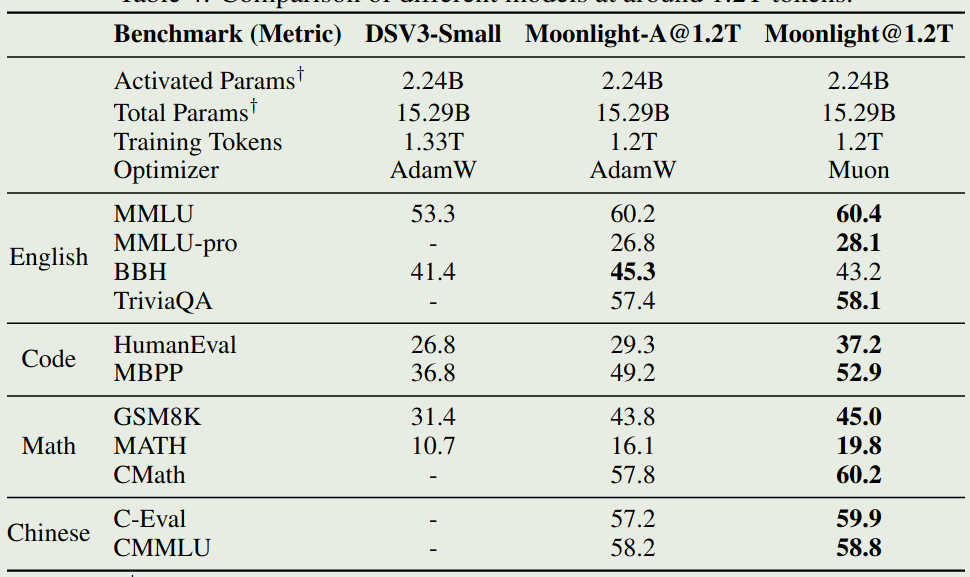
Pretraining performance of different optimizer

可以看到，在相同的设置下，Muon optimizer 的表现更好。

Dynamics of Singular Spectrum

Muon optimizer 的核心思想就是让比较难更新的方向也能被更新到，本节作者就探究了 Muon 是否满足这个性质，作者对参数矩阵进行 SVD 分解，然后定义 SVD entropy 如下

$$ H(\sigma) = -\frac{1}{\log n}\sum_{i=1}^n\frac{\sigma_i^2}{\sum_{j=1}^n\sigma_j^2}\log\frac{\sigma_i^2}{\sum_{j=1}^n\sigma_j^2} $$

作者对 SVD entropy 可视化如下

Visualization of SVD entropy

可以看到，Muon optimizer 的 SVD entropy 比 AdamW 更大，这说明 AdamW 的更新方向更多更广，验证了 Muon optimizer 的核心思想

SFT with Muon

作者还在 SFT 阶段验证了 Muon optimizer 的有效性。实验结果如下图所示

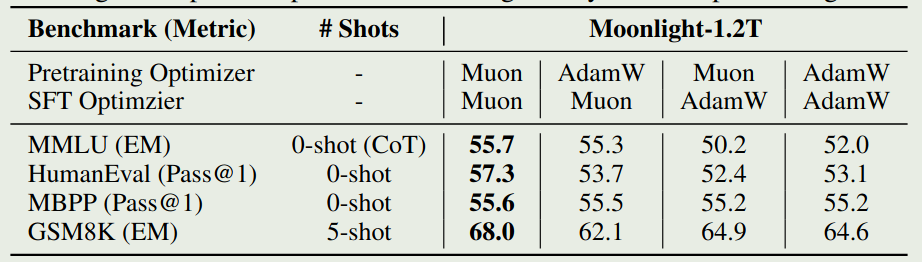
Performance of Muon on SFT stage

结论主要有两个：

预训练阶段与 SFT 阶段使用不同的优化器时，模型表现没有明显区别
SFT 阶段使用 Muon 可以达到与 AdamW 差不多的表现，但是最好还是在 pre-training 阶段使用 Muon

Conclusion

作者探究了如何 scale up Muon Optimizer. 通过改进，作者在 16B-A3B 的 MoE LLM 上验证了 Muon Optimizer 的性能。实验结果发现，Muon Optimizer 的训练效率比 AdamW 提升了 2 倍左右。

作者提出了三个未来可行的研究方向：

目前 Muon 只能针对 2D 参数进行优化，其他参数仍然依赖于 AdamW 优化器，是否可以使用 Muon 优化所有参数？
Muon optimizer 可以理解是 spectral norm 下的 steepest descent 方法，如何将其扩展到 Schatten norm 是一个可以研究的方向
实验里提到，预训练和 SFT 阶段使用不同的 optimizer, 表现不是最优的，如何解决这个因为不同 optimizer 导致的性能差距是一个需要解决的问题。

References

Muon is Scalable for LLM Training