DeepSeek 在 25 年 1 月提出了 Natively trainable Sparse Attention (NSA), 一个软硬件结合的稀疏注意力机制,NSA 可以在提高模型推理效率的同时提高计算效率。
Introduction
现有的大模型主要是基于 Transformer 提出的 softmax attention, 其主要问题在于随上下文长度增加,其 latency 也上升更快。理论估计,对于 64k 上下文长度的输出,softmax attention 部分的计算占 $70\%\sim80\%$ 的 latency.
为了解决 softmax 的 high latency 问题,,一个做法就是使用稀疏注意力机制,如 MInference 等,但是这些系数注意力机制大多没有实际部署,且它们一般只在 inference 阶段使用
作者认为解决这个问题有两个挑战:
- Hardware-aligned inference speedup: 降低 inference latency 需要算法与硬件结合,不能只关注算法层面的改进
- Training-aware algorithm design: 需要在训练阶段也支持算法,从而可以降低训练的算力消耗并且保持模型的表现
为了解决这两个问题,作者就提出了 natively trainable sparse attention (NSA) 架构。NSA 通过将 key 和 value 分割为不同的 block, 然后基于三种 path: compressed coarse-grained tokens, selectively retrained fine-grained tokens 以及 sliding windows for local contextual information 来进行处理和过滤。NSA 提出了两点观点改进:
- Hardware-aligned system: 优化了 blockwise sparse attention 来平衡 arithmetic intensity.
- Training-aware design: 支持端到端的训练和部署
Method
Overview
作者首先回顾了 attention 的定义如下:
$$ \mathbf{o}_t=\mathrm{Attn}(\mathbf{q_t},\mathbf{k}_{:,t}, \mathbf{v}_{:,t})=\sum_{i=1}^t \frac{\alpha_{t,i}}{\sum_{t,i}\alpha_{t,i}}\mathbf{v_i},\ \alpha_{t,i} = \exp\left(\frac{\mathbf{q_t}^T\mathbf{k}_{i}}{\sqrt{d_k}}\right) $$其中 $\mathbf{q_t}\in\mathbb{R}^{d_k}$.
接下来是 Arithmetic Intensity. Arithmetic intensity 指的是 FLOPs 与内存访问次数之比。由于现在的 GPU 都是计算密集型设备,理想情况下应该是 Arithmetic intensity 越高越好。
对于 causal self-attention 来说,在训练以及 prefilling 阶段,由于 batch 较大,因此整体的 Arithmetic intensity 较高,因而这两个阶段是 computer-bound. 但是在 decoding 阶段,由于其 token-by-token generation 的性质,每次生成新的 token 时都需要重新加载 KV cache, 因而是 memory-bound.
从而我们的优化目标也变得不一致:在训练阶段,我们希望降低计算消耗,而在推理 (decodng) 阶段,我们希望降低内存访问次数。
基于这两个目标,作者提出了使用 $\mathbf{k}_{:,t}, \mathbf{v}_{:,t}$ 的子集 $\tilde{K}_t, \tilde{V}_t$ 来参与计算,其对应的 attention 如下所示
$$ \tilde{K}_t=f_K(\mathbf{q_t},\mathbf{k}_{:,t}, \mathbf{v}_{:,t}), \tilde{V}_t=f_V(\mathbf{q_t},\mathbf{k}_{:,t}, \mathbf{v}_{:,t}), \mathbf{o}_t=\mathrm{Attn}(\mathbf{q_t},\tilde{K}_t, \tilde{V}_t) $$我们还可以结合不同的方法来进行组合:
$$ \mathbf{o}_t^*=\sum_{c\in\mathcal{C}}g_t^c\mathrm{Attn}(\mathbf{q_t},\tilde{K}_t^c, \tilde{V}_t^c) $$作者在本文中使用了三种方法 $\mathcal{C}=\{\mathrm{cmp},\mathrm{slc},\mathrm{win}\}$, 分别代表了 compression, selection 以及 sliding window, $g_t^c\in[0,1]$ 代表了不同方法对应的 gating score, 类似于 MoE 的 gating layer, $g_t^c$ 由一个 MLP 和一个 sigmoid activation 生成。最终 NSA 的架构如下图所示
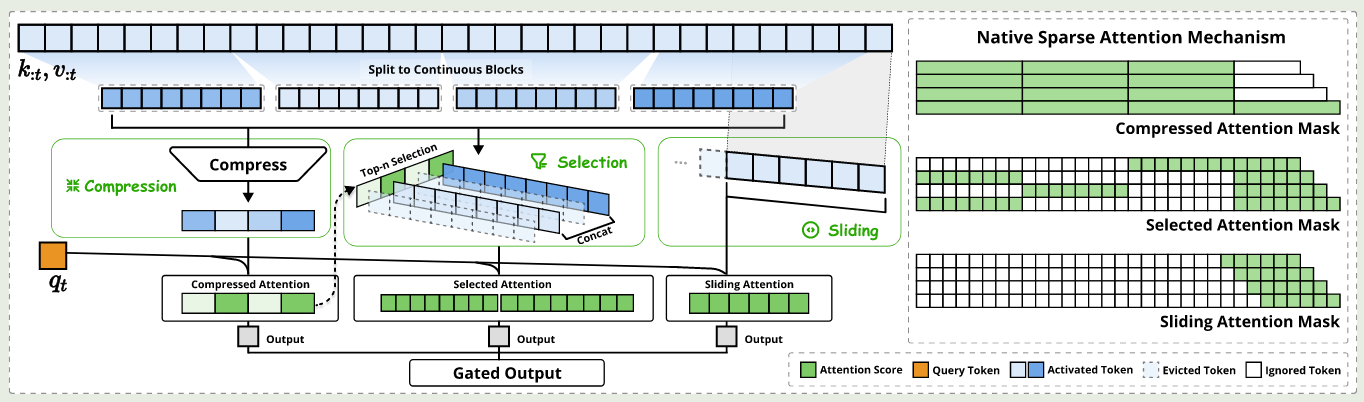
作者定义 $N_t$ 代表参与计算的 KV 的总个数:
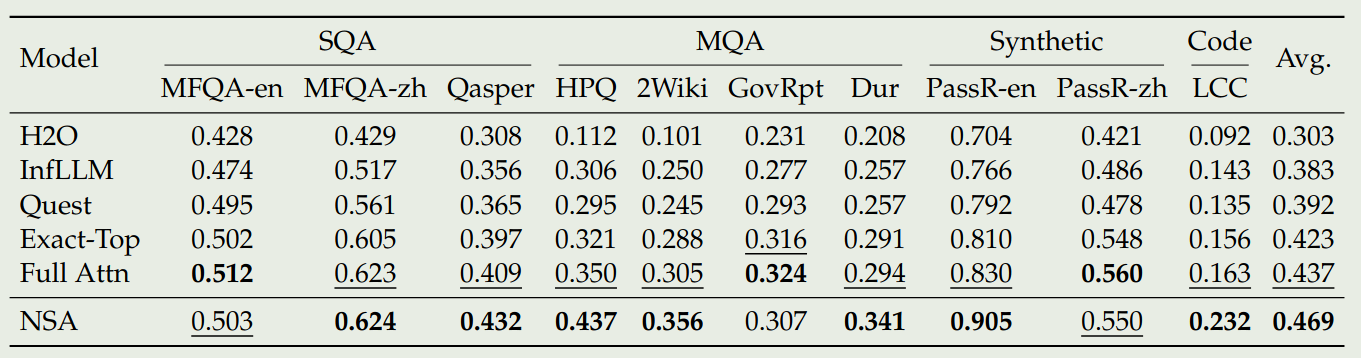
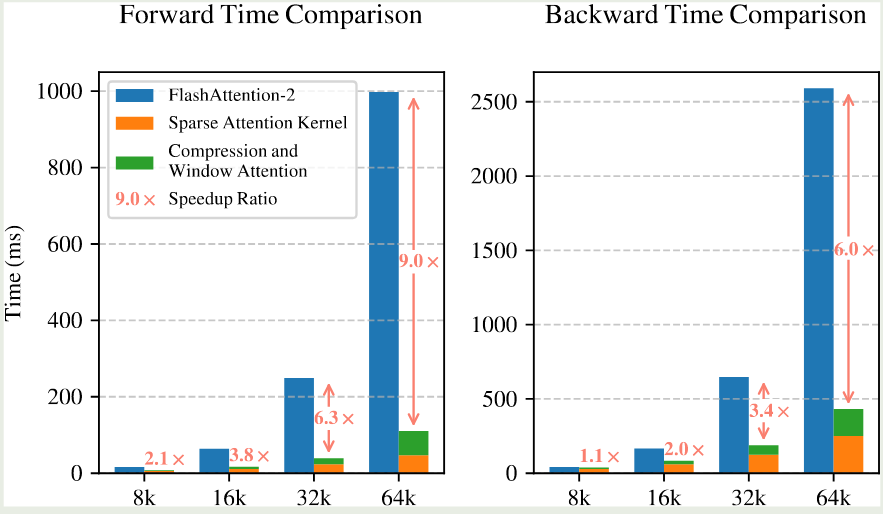
$$ N_t = \sum_{c\in\mathcal{C}} \mathrm{size}[\tilde{K}_t^c]. $$作者使用了一个较高的 sparsity ratio 来保证 $N_t< 接下来作者分别介绍了每一部分的设计 对于 token compression, 其定义如下: 其中 $l$ 是 block size, $d$ 是 sliding stride, $\phi:\mathbb{R}^{l\times d_k}\to \mathbb{R}^d_k$ 是一个 MLP 用于将 block key 映射为一个单一的 key. 对于 $\tilde{V}_t^{\mathrm{cmp}}$ 作者也使用了类似的做法。 仅使用 compressed token 的话,可能会丢失一些细粒度的信息。因此,作者额外提出了 token selection 机制来解决这个问题。 作者使用的做法是 blockwise selection. 这样做的原因有两点: 为了实现 block-wise selection, 作者首先将 key value sequences 分割为 blocks, 然后针对每个 blocks 分配 Importance score. 作者首先介绍了如何计算不同 block 的 importance score. 如果 selection block size 与 compression block size ,即 $l'=l$ 相同的话,则我们可以直接用 compression block 提供的信息: 其中 $\mathbf{p}_{t}^{\mathrm{cmp}}\in\mathbb{R}^{\left\lfloor\frac{t-l}{d}\right\rfloor+1}$ 代表了 $\mathbf{q}_t$ 和 compressed key $\tilde{K}_t^{\mathrm{cmp}}$ 之间的 attention score. 如果 $l'\neq l$ 的话,作者通过空间关系来进行计算,假设 $l\leq l'$, $d\mid l$, $d\mod l'$, 则我们有 对于 GQA 和 MQA, 由于其 KV-cache 在 heads 之间共享,因此我们必须保证不同 heads 之间的 consistency, 因此作者提出了 shared importance score 如下: 接下来,对于每个 block 及其对应的 Importance score, 作者保存 top-$n$ sparse blcoks, 如下所示 其中 $\mathrm{rank}(\cdot)$ 代表了降序排列的 importance scores. $\mathcal{I}_t$ 是选择出来的 block indices, $\mathrm{Cat}(\cdot)$ 表示了 concatenation operation. $\tilde{K}_t^{\mathrm{slc}}\in\mathbb{R}^{d_k\times il'}$ 代表了选择出来的 key. 为了避免 local pattern 对 compression token 以及 selection token 的学习产生影响,作者额外使用了一个 branch 来学习这个 local pattern. 其具体做法就是维持一个 sliding window 用于最近的若干个 token, 即 这里 $w$ 是 window size. 为了进一步避免 shortcut learning, 对于三个 branch 作者提供了不同的 key 和 values 接下来是针对硬件设计进行的优化。由于 flash attention 2 对 compression attention 以及 sliding window attention 已经支持的比较好,作者这里介绍了如何针对 selection attention 进行优化。 作者构建了一个 27B-A3B 的 MoE 模型,attention 基于 GQA, MoE 基于 DeepSeekMoE. 模型配置如下表所示 NSA 配置如下 其中 selection blocks 包含初始的一个 block 以及最近的 2 个 block. 模型先在 8K 的上下文长度下使用 270B token 进行预训练,接下来在使用 YARN 将模型上下文通过 continual pre-training 以及 SFT 扩展到 32K. 训练过程的损失如下图所示 作者从 general performance, long-context performance 以及 CoT reasoning performance 三个层面来评估 NSA 的表现。 首先是 NSA 与其他 sparse attention 以及 baseline 在通用任务上表现的对比,结果如下图所示 接下来是 NSA 在 LongBench 上的表现: 作者还使用了 DeepSeek-R1 中的知识蒸馏方法,结果如下表所示 上面的结果均验证了 NSA 的有效性 接下来,作者分析了 NSA 的性质。作者首先对比了 NSA 和 flash attention 2 的训练速度,结果如下图所示 可以看到,相比于 flash attention 2, NSA 在 forward 过程和 backward 过程的的效率分别提升了 9 倍和 6 倍。作者认为这是由于两个优点: 作者还对比了不同 attention 的解码速度,在 NSA 中,每次只需要 $\left\lfloor\frac{s-l}{d}\right\rfloor+nl'+w$ 个 token 就可以完成计算,作者对比不同 attention 所需余姚的 token 如下表所示如下表所示 作者在本文中提出了 NSA, 一个通过软硬件协同结合 compression, selection 以及 sliding window 的稀疏注意力机制,作者通过实验验证了其有效性。Design
Token Compression
Token Selection
Sliding Window
Kernel Design
Experiments
field value layers 30 hidden dimension 2560 head groups 4 attention heads 64 query head dimension 192 value head dimension 128 routed experts 72 shared experts 2 activated experts 6 dense layers 1 field value $l$ 32 $d$ 16 $l'$ 64 $n$ 16 $w$ 512 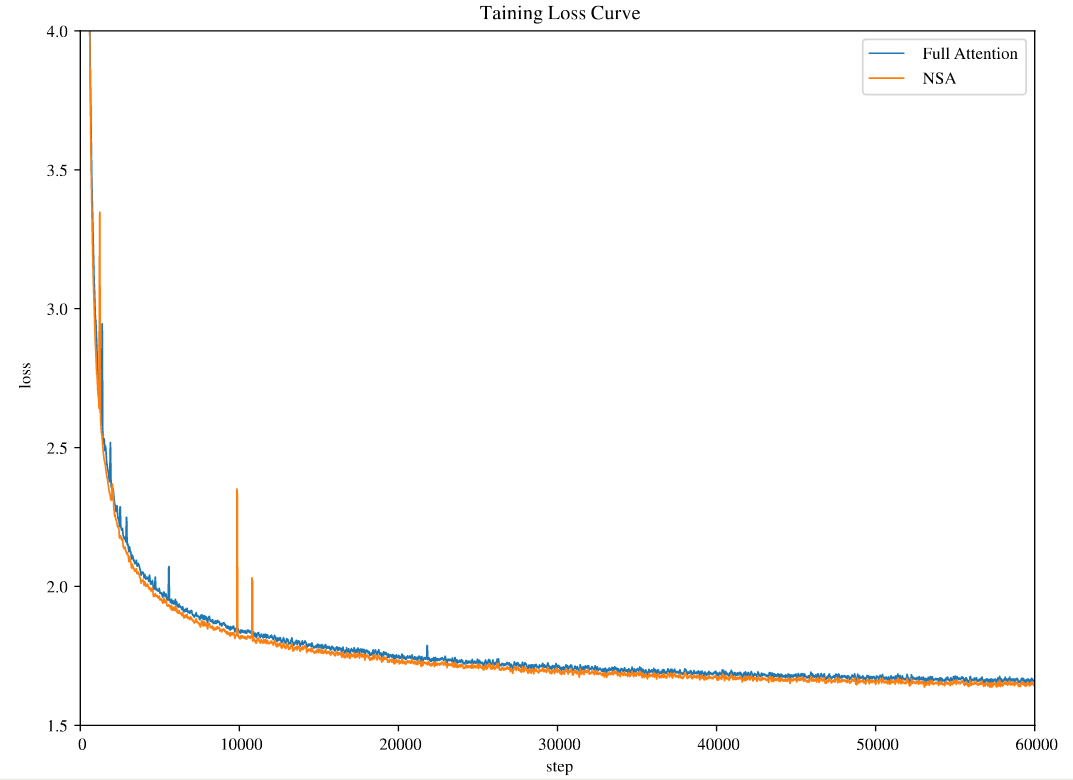

Generation token limit 8192 16384 Full Attention-R 0.046 0.092 NSA-R 0.121 0.146 Analysis
Context Length 8192 16384 32768 65536 Full attention 8192 16384 32768 65536 NSA 2048 2560 3584 5632 speedup 4x 6.4x 9.1x 11.6x Discussion
Conclusion
References