Introduction
相关工作包括 GRPO 以及 GSPO
SAPO 的关键思想有两点:
- tokne-level soft trust region 可以保证 sequence-level coherence
- 非对称的 temperature 可以针对 postive token 和 negative token 进行不同的优化
Method
作者首先给出了 SAPO 的目标函数如下:
$$ \mathcal{J}_{\mathrm{SAPO}}(\theta) = \mathbb{E}_{(x, y)\sim\mathcal{D},\{y_i\}_{i=1}^G\sim \pi_{\theta_{old}}(\cdot\mid x)}\left[ \frac{1}{G}\sum_{i=1}^G\frac{1}{|y_i|}\sum_{t=1}^{|y_i|}f_{i,t}(r_{i,t}(\theta))\hat{A}_{i,t} \right], $$其中,
$$ f_{i,t}(x) = \sigma(\tau_{i,t}(x-1))\cdot \frac{4}{\tau_{i,t}}, \tau_{i,t} = \begin{cases} \tau_{pos}, & \text{if }\hat{A}_{i,t}>0\\ \tau_{neg}, &\text{otherwise} \end{cases} $$这里
$$ \hat{A}_{i,t} = \hat{A}_{i} = \frac{r(x,y_i) - \mathrm{mean}(\{r(x,y_i)\}_{i=1}^G)}{\mathrm{std}(\{r(x,y_i)\}_{i=1}^G)},\quad r_{i,t}(\theta) = \frac{\pi_{\theta}(y_{i,t}\mid x, y_{i,< t})}{\pi_{\theta_{old}}(y_{i,t}\mid x, y_{i,< t})} $$$\tau_{pos}$ 和 $\tau_{neg}$ 分别是 positive token 以及 negative token 对应的温度, $\sigma(x)=1/(1+e^{-x})$ 是 sigmoid function.
对 $\mathcal{J}_{\mathrm{SAPO}}(\theta)$ 求导得到
$$ \nabla_\theta \mathcal{J}_{\mathrm{SAPO}}(\theta) = \mathbb{E}_{(x, y)\sim\mathcal{D},\{y_i\}_{i=1}^G\sim \pi_{\theta_{old}}(\cdot\mid q)}\left[ \frac{1}{G}\sum_{i=1}^G\frac{1}{|y_i|}\sum_{t=1}^{|y_i|}w_{i,t}(\theta)r_{i,t}(\theta)\nabla_\theta \log \pi_\theta(y_{i,t}\mid q, y_{i,$\mathcal{J}_{\mathrm{SAPO}}(\theta)$ 和 $w_{i,t}(\theta)$ 与 $r_{i,t}(\theta)$ 的关系如下图所示
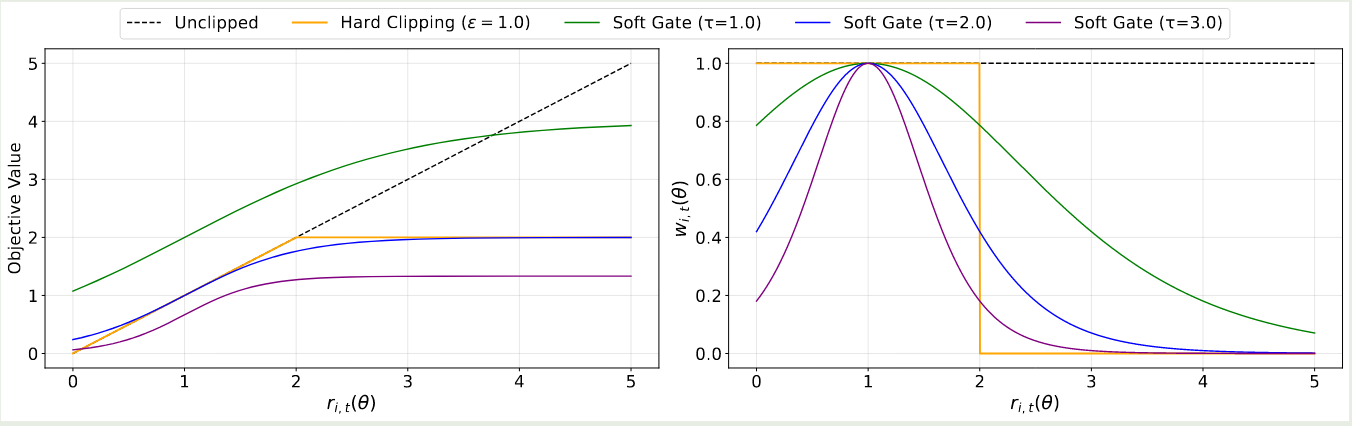
为了保证当 $r_{i,t}(\theta)=1$ 时,SAPO 等价于 $r_{i,t}(\theta)\hat{A}_{i,t}$ 而与 $\tau_{i,t}$ 无关,作者在 $f_{i,t}(x)$ 加入了系数 $4/\tau_{i,t}$.
Comparison
作者接下来对比了 GSPO 以及 GRPO 两个算法
首先作者使用了一下统一的目标函数公式来表示三个算法
$$ \mathcal{J}(\theta) = \mathbb{E}_{(x, y)\sim\mathcal{D},\{y_i\}_{i=1}^G\sim \pi_{\theta_{old}}(\cdot\mid x)}\left[ \frac{1}{G}\sum_{i=1}^G\frac{1}{|y_i|}\sum_{t=1}^{|y_i|}f_{i,t}(r_{i,t}(\theta))\hat{A}_{i,t} \right], $$其中不同算法的 $f_{i,t}(\cdot)$ 不一样,三种算法的定义如下
$$ \begin{aligned} \mathrm{SAPO}&:f_{i,t}^{\mathrm{SAPO}}(r_{i,t}(\theta))=\sigma(\tau_{i,t}(x-1))\cdot \frac{4}{\tau_{i,t}}, \tau_{i,t} = \begin{cases} \tau_{pos}, & \text{if }\hat{A}_{i,t}>0\\ \tau_{neg}, &\text{otherwise} \end{cases}\\ \mathrm{GRPO}&:f_{i,t}^{\mathrm{GRPO}}(r_{i,t}(\theta), \hat{A}_{i,t})=\begin{cases} \min(r_{i,t}(\theta), 1+\epsilon) & \hat{A}_{i,t}>0\\ \max(r_{i,t}(\theta), 1-\epsilon) & \hat{A}_{i,t}\leq0 \end{cases}\\ \mathrm{GSPO}&:f_{i,t}^{\mathrm{GSPO}}(r_{i,t}(\theta), \hat{A}_{i,t})=f_{i,t}^{\mathrm{seq}}(r_{i,t}(\theta), \hat{A}_{i,t})=\begin{cases} \min(s_{i,t}(\theta), 1+\epsilon) & \hat{A}_{i,t}>0\\ \max(s_{i,t}(\theta), 1-\epsilon) & \hat{A}_{i,t}\leq0 \end{cases} \end{aligned} $$其中
$$ s_i(\theta) = \left(\frac{\pi_{\theta}(y_{i}\mid x)}{\pi_{\theta_{old}}(y_{i}\mid x)}\right)^{\frac{1}{|y_i|}}, s_{i,t}(\theta) = \mathrm{sg}[s_i(\theta)]\frac{\pi_{\theta}(y_{i,t}\mid x, y_{i,< t})}{\mathrm{sg}[\pi_{\theta}(y_{i,t}\mid x, y_{i,< t})]} $$首先是与 GSPO 的对比,通过一些假设和简化,我们得到
$$ \begin{aligned} \nabla_\theta \mathcal{J}_{\mathrm{SAPO}}(\theta) &=\mathbb{E}\left[\frac1G\sum_{i=1}^G g_{\tau_i}(\log s_i(\theta))\nabla_\theta \log s_i(\theta)\hat{A}_i\right]\\ \nabla_\theta \mathcal{J}_{\mathrm{GSPO}}(\theta) &=\mathbb{E}\left[\frac1G\sum_{i=1}^G s_i(\theta)\nabla_\theta \log s_i(\theta)\hat{A}_i\right] \end{aligned} $$其中 $g_{\tau_i}(\log s_i(\theta)) = \mathrm{sech}^2\left(\tau_i/2\log s_i(\theta)\right)$. 相比于 GSPO, SAPO 有两个优势:
- smoothness and stability, soft gate 避免了 hard clipping 带来的不连续性
- token-level adaptivity with sequence-level coherence. 当假设不成立的时候,SAPO 退化为 token-level gating, 这样可以降低 outliers 的权重
GRPO 的函数可以进一步简化为
$$ f_{i,t}^{\mathrm{GRPO}}(r_{i,t}(\theta), \hat{A}_{i,t})= \begin{cases} 1, & \text{if }\hat{A}_{i,t}>0\text{ and }r_{i,t}(\theta)\leq 1+ \epsilon\\ 0, & \text{if }\hat{A}_{i,t}>0\text{ and }r_{i,t}(\theta)> 1+ \epsilon\\ 1, & \text{if }\hat{A}_{i,t}\leq0\text{ and }r_{i,t}(\theta)\geq 1- \epsilon\\ 0, & \text{if }\hat{A}_{i,t}\leq0\text{ and }r_{i,t}(\theta)< 1- \epsilon \end{cases}\\ $$可以看到,GRPO 对应一个 binary trust region. 与 GRPO 相比,SAPO 将对应的 hard indicator 替换未来一个 smooth kernel $f_{i,t}^{\mathrm{SAPO}}(r_{i,t}(\theta))=\mathrm{sech}^2\left(\tau_i/2r_{i,t}(\theta)-1\right)$, 这样可以避免 gradient vanishing 以及提高训练的稳定性。
最终结论为:
- 相比于 GSPO, SAPO 对于 off-policy 的数据利用率更高
- 相比于 GRPO, SAPO 避免了 hard token level clipping 导致的 zero-gradient 问题
Experiments
作者对比了 SAPO, GSPO 以及 GRPO-R2(GRPO with routing replay) 三种方法,实验结果如下图所示
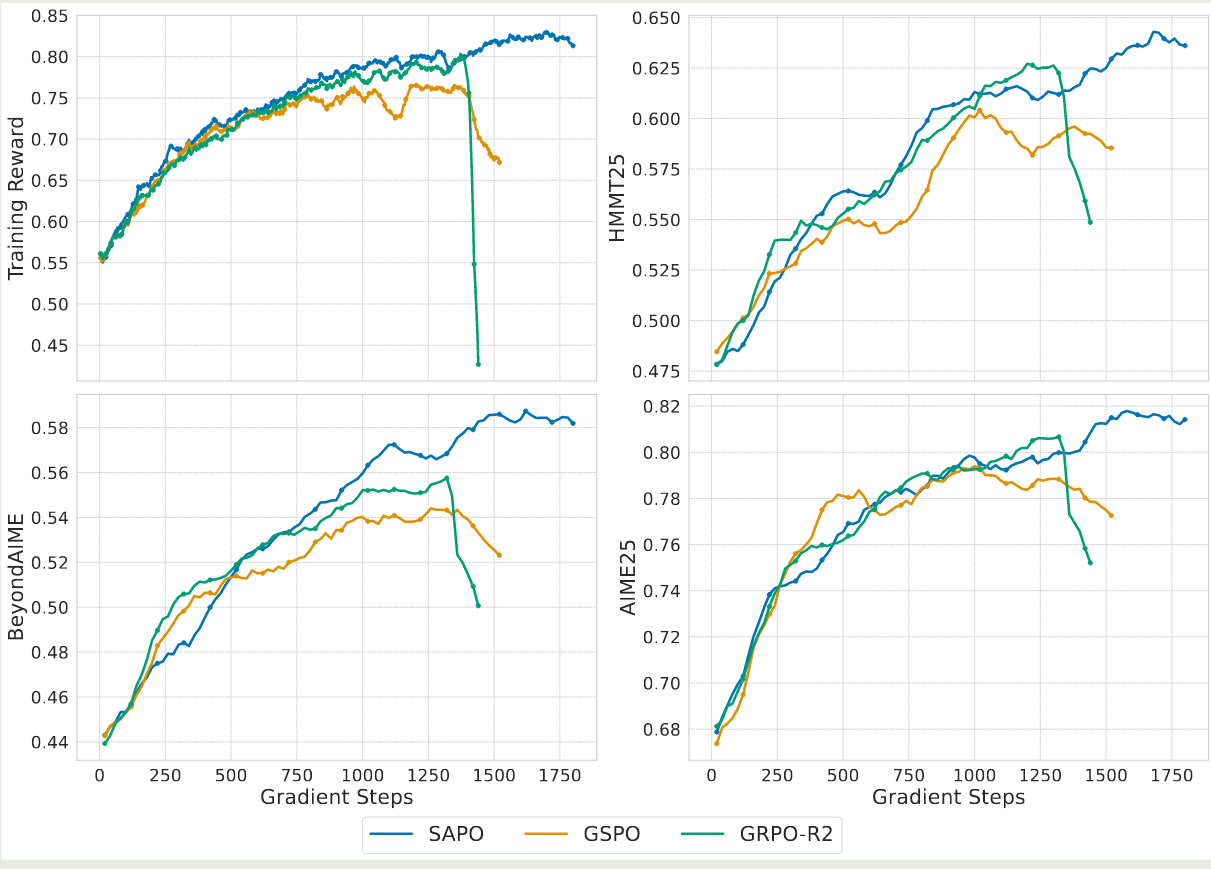
实验结果显示,SAPO 的表现超过了 GSPO 以及 GRPO
作者还探究了超参数 $\tau_{pos}$ 和 $\tau_{neg}$ 的影响,结果如下图所示
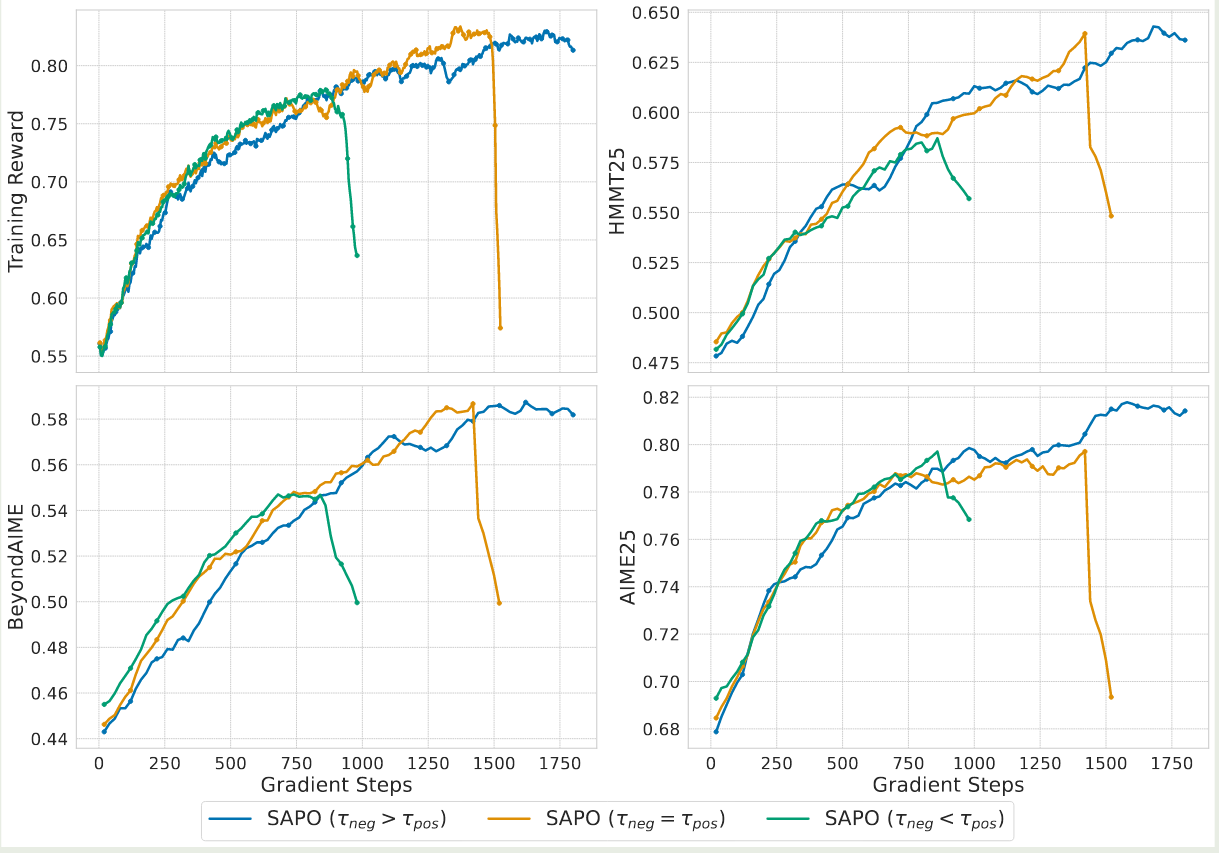
实验结果显示,当 $\tau_{neg}>\tau_{pos}$ 时,模型训练最稳定,这说明了 negative token 是导致训练不稳定的主要原因。
作者还在 Qwen3-VL 上进行了验证,结果如下图所示
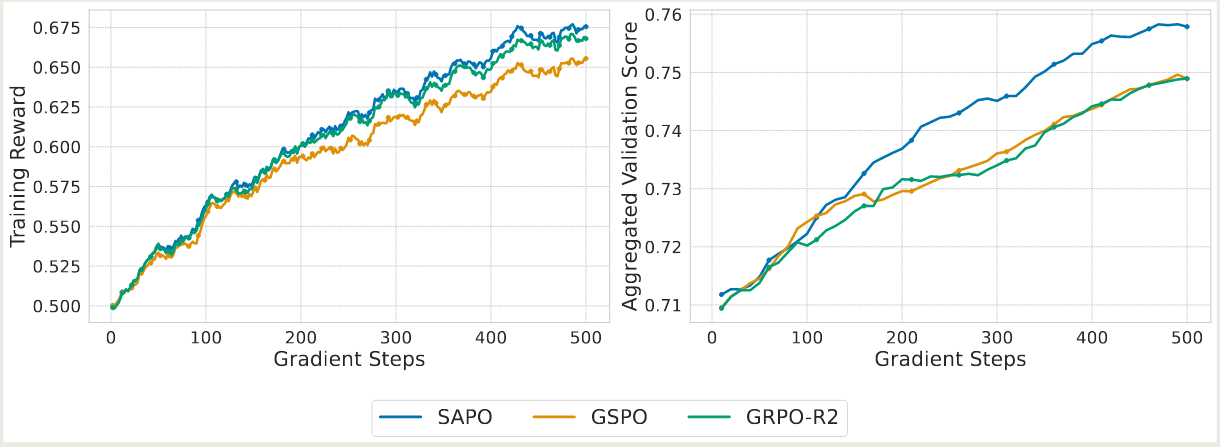
实验结果显示,SAPO 的表现超过了 GSPO 以及 GRPO-R2
Conclusion
在本文中,作者提出了 SAPO, 一个解决 hard-clipping 训练不稳定性以及低效率的策略优化算法,作者使用了基于温度的 soft gate 来代替 clipping, 以及对于 positive token 和 negative token 使用了不同的 temperature 这两点改进。结果验证了 SAPO 的有效性,作者认为使用 smooth 以及 adaptive gating 机制可以有效提高 RL 训练的稳健性以及有效性。