Introduction
YaRN (Yet Another RoPE extentionN method) 时23年9月EleutherAI等提出来的一个扩展LLM上下文长度的方法,后来被Qwen系列模型所应用。
Preliminary
作者首先回顾了一下RoPE, 具体内容请参见上一篇blog。并使用了 $f_{W}(x_m, m, \theta_d)$ 来表示RoPE:
$$ f_{W}(x_m, m, \theta_{d}) = \Theta_{\theta, m}^d W x_m $$其中 $\Theta_{\theta, m}^d\in\mathbb{R}^{d\times d}$ 是多维旋转矩阵, $\theta_d=[\theta_{0,d},\dots,\theta_{(d-2)/2,d}]\in\mathbb{R}^{d/2}$, $\theta_{i,d}=\theta^{2i/d}$, $\theta>0$ 是一个超参数,RoPE中设置为 $\theta=10000$, $W\in\{W_q,W_k\}\subset\mathbb{R}^{d\times d}$ 是对应的query/key projection layer的权重矩阵, $x\in\mathbb{R}^{d}$ 是输入的hidden states.
接下来,作者定义了两个新的变量:
scaling factor 假设预训练的上下文长度为 $L$, 扩展的上下文长度为 $L'>L$, 则我们定义scaling factor 为
$$ s = \frac{L'}{L} $$易知 $s>1$.
wavelength 我们将 $\lambda_d$ 定义为 $i$-th 维的RoPE embedding对应的 wavelength:
$$ \lambda_{i,d} = \frac{2\pi}{\theta_{i,d}} = 2\pi\theta^{2i/d}, \ i=0,\dots,(d-2)/2 $$wavelength描述了对于第$i$ 个维度,RoPE旋转一周 ($2\pi$) 所需要的上下文长度。
Unified Perspective on Related Work
基于 $f_{W}(x_m, m, \theta_d)$, 作者统一了已有的扩展上下文长度的方法,作者将不同的扩展方法使用一个通用函数 $f_W(x_m,g(m), h(\theta_d))$ 来表示,这里 $g(m)$ 和 $h(\theta_d)$ 分别代表了不同的长度外推方法所使用的变换。
Position Interpolation
Position Interpolation (PI) 的核心思想在于,我们可以通过Interpolation,将超过预训练长度的文本给压缩到当前最大长度,以此来避免RoPE外推产生的问题,其对应的公式为
$$ f'_W(x_m,m,\theta_d) = f_W(x_m, \frac{mL}{L'}, \theta_d) $$其中 $L'>L$ 为我们扩展之后的上下文长度, $L$ 为我们预训练的上下文长度。使用通用函数表示的话,我们有
$$ g(m) = \frac{m}{s},\quad h(\theta_d) = \theta_d $$NTK-aware Interpolation
PI的问题是,并没有考虑不同维度的wavelength。 基于NTK理论,DNN当输入维度比较低,且embedding缺少高频内容时,模型就会很难学习到高频信息。对应到RoPE里面,输入的token position id是低位信息(1维),而输出的RoPE是一个 $d$ 维的复杂向量。因此,当输入token非常相似却距离非常近时,RoPE就会丢失高频的细节信息
因此,为了解决这个问题,作者对不同的维度使用了不同的缩放策略:维度比较小时,其缩放的更多,维度比较大是,其缩放的更少。
基于这个策略,作者提出了NTK-aware interpolation,其定义如下:
$$ g(m) = m, \quad h(\theta_{i,d}) = \theta'^{-2i/d}, i=0,\dots,(d-2)/2 $$其中
$$ \theta' = \theta\cdot s^{\frac{d}{d-2}} $$实际中,这种方法会产生out-of-bound的值,因此最终结果会比PI要差一点,为了解决这个问题,一般会使用比 $s$ 更大的scaling factor.
上式的推导基于一个简单的假设:我们希望最后一个维度的wavelength在scaling之后,是线性变化的,即 $\theta'_{(d-2)/2,d}=s\theta_{(d-2)/2,d}$, 求解之后,我们就得到了上面的定义
PI 和NTK-aware interpolation的问题在于,我们对不同的维度的处理都是一样的。这类不在乎wavelength的方法被称为blind interpolation methods, 接下来要介绍的就是基于wavelength的方法,即target interpolation methods.
NTK-by-parts Interpolation
与NTK-aware interpolation, NTK-by-parts interpolation基于wavelength来考虑不同维度上所做的变换。
对于低维度,其 $\theta_{i,d}$ 非常大,因此旋转一周所需要的上下文长度也非常大。实际上就导致某些维度的embedding并不是均匀分布的,(比如说只有 $0\sim\pi$ 这个区间的embedding),这个时候,模型就只能访问到绝对位置信息,而访问不到相对位置信息。 另外,当我们对所有的维度都进行scale的时候,所有的token都会与彼此更加靠近,这损害了模型对于局部信息的获取能力。 基于这些认知,作者基于wavelength,对不同的维度分别进行处理:
- 如果wavelength远小于上下文长度 $L$, 则我们不做任何处理
- 如果wavelength等于或者大于上下文长度 $L$, 则我们使用NTK-aware interpolation 进行处理
- 对于中间的其他维度,我们进行了一个trade off
作者定义了一个ratio $r$ 来描述原始上下文长度 $L$ 和 wavelength 之间的关系
$$ r(i,d) = \frac{L}{\lambda_{i,d}} = \frac{L}{2\pi\theta'^{2i/d}} $$基于这个ratio,我们可以定义上面的三种处理方式对应的权重
$$ \gamma(r) = \begin{cases} 0, &\text{if } r < \alpha\\ 1, &\text{if } r > \beta\\ \frac{r-\alpha}{\beta-\alpha}, &\text{otherwise} \end{cases} $$其中, $\beta>\alpha>0$ 是超参数, $r<\alpha$, $r<\beta$ 分别代表了上面的第1种,第2种情况。
最后,NTK-by-parts interpolation的定义如下
$$ g(m) = m, \quad h(\theta_i) = \left(1-\gamma(r(i,d)\right)\frac{\theta_i}{s} + \gamma(r(i,d))\theta_i $$作者通过实验发现,在LLaMA上,$\alpha=1$ 和 $\beta=32$ 是一个比较好的选择
Dynamic NTK Interpolation
在实际中,一个经常遇到的场景就是sequence length会从1逐步上升到最大上下文长度,比如说inference的时候。对于这种情况,我们有两种解决方法:
- 在整个inference周期中,RoPE的scaling factor都设置为 $s=K'/L$, 其中$L'$ 是扩展后的上下文长度
- 在每次foward的过程汇总,都更新sclaing factor $s=\max(1, \ell'/L)$, 这里 $\ell'$ 是当前sequence的长度
作者发现,方案1在sequence长度小于 $L$的时候性能会下降,并且当上下文长度超过 $L'$ 时,性能下降的更快。 但是,方案2可以让模型的性能下降曲线更平缓。因此,作者将这种inference-time方法称为 Dynamic Scaling method, 当其与NTK-aware方法结合时,就得到了 Dynamic NTK interpolation
作者通过实验发现,Dynamic NTK interpolation在$L'=L$ 时,效果非常好
YaRN
在YaRN中,作者针对Dynamic NTK interpolation做了进一步改进,也就是在计算attention softmax时,加入了一个温度参数 $t>0$, 这样attention的计算就变成了
$$ \mathrm{Attn}(Q, K, V) = \mathrm{softmax}\left(\frac{QK^T}{t\sqrt{d}}\right)V $$作者发现,通过这种scaling的方式,YaRN可以在不改变代码的前提下,更改attention的机制。并且,其不增加训练和推理的cost
作者将YaRN定义为结合了NTK-by-parts interpolation和上述scaling技巧的方法
对于LLaMA,作者推荐使用如下参数:
$$ \sqrt{\frac{1}{t}} = 0.1\ln(s) + 1. $$实验结果如下
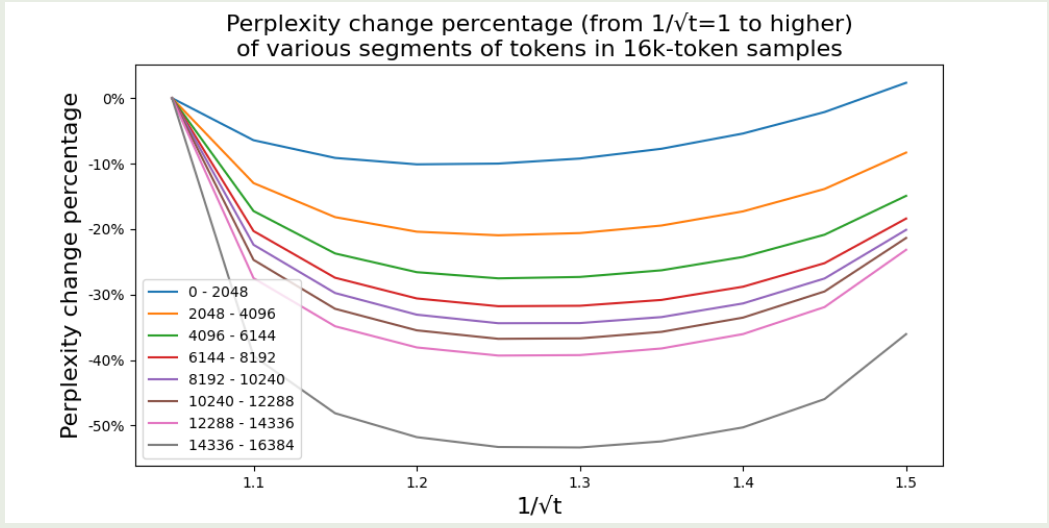
作者发现:
- 对于合适的 $t$, 扩展上下文之后,perplexity会变的更好
- 最好的$t$ 对于不同的位置和样本提升都是一样的
Evaluation
实验结果如下
| Extension Method | Trained Tokens | Context Window | Evaluation Context Window Size | |||||
|---|---|---|---|---|---|---|---|---|
| 2048 | 4096 | 6144 | 8192 | 10240 | ||||
| PI (s = 2) | 1B | 8k | 3.92 | 3.51 | 3.51 | 3.34 | 8.07 | |
| NTK ($\theta$ = 20k) | 1B | 8k | 4.20 | 3.75 | 3.74 | 3.59 | 6.24 | |
| YaRN (s = 2) | 400M | 8k | 3.91 | 3.50 | 3.51 | 3.35 | 6.04 |
可以看到,YaRN使用的数据更少,并且当模型扩展到10240的时候,其表现下降的最慢,这说明了YaRN在扩展上下文长度时的有效性
原始RoPE,dynamic-PI和dynamic-YaRN的对比
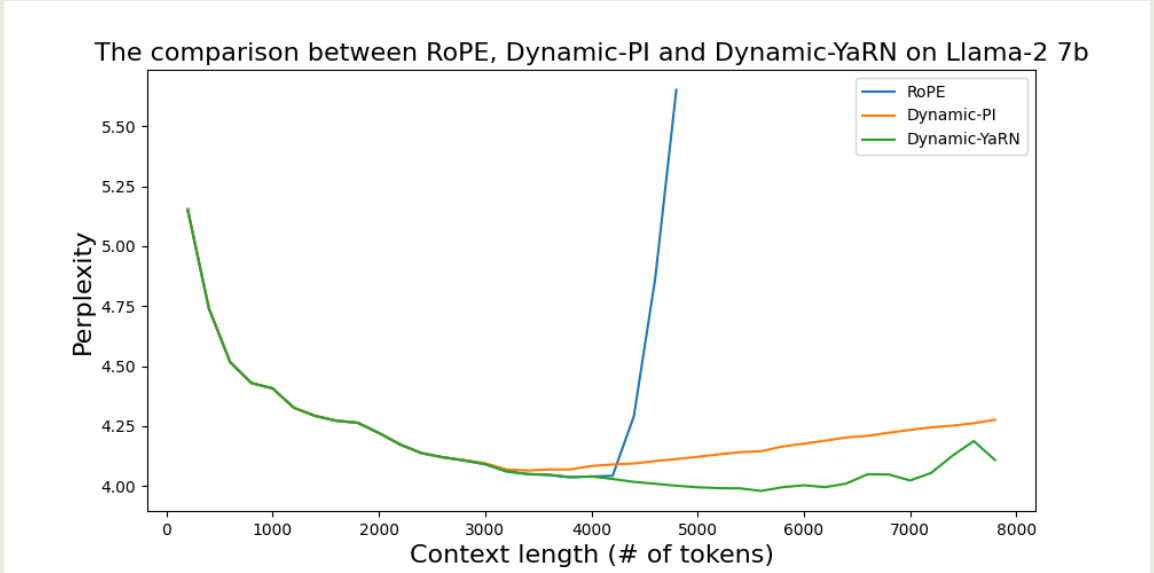
可以看到,RoPE的上下文扩展能力很差,Dynamic-YaRN的表现最好。
Code
YaRN的实现在HuggingFace/src/transformers/modeling_rope_utils.py 里的 _compute_yarn_parameters 函数里,其返回 inv_freq 以及 attention_factor 两个量,前者代表了 $\theta_d$, 后者代表 $t\sqrt{d}$.
| |
实际的transformers代码中,Qwen使用的还是默认的RoPE,在inference时如果我们需要扩展上下文,可以通过修改config的形式:
| |
Conclusion
在本文中,作者首先构建了一个统一的表征不同上下文长度扩展的形式,接下来作者分析了不同上下文长度扩展的不足,并提出了YaRN这种上下文长度扩展方式,结果发现,YaRN不仅在短上下文长度下面表现很好,当上下文长度扩展之后,其表现依然非常优秀。