Introduction
已有的工作如 GShard 和 Switch Transformer 均验证了 MoE 模型的有效性,但是他们的问题在于训练不稳定。
因此,在本文中,作者就提出了 ST-MoE 来解决这个问题。作者的主要贡献如下:
- 探究了如何平衡模型的表现与训练稳定性
- 提出了 router Z-loss 来解决训练的不稳定性
- 探究了如何设定 MoE 模型 fine tuning 时的超参数
- 对 MoE 的性质进行了分析
Training Stability
作者发现,直接训练 MoE 模型会面临训练不稳定性的问题,实验结果如下图所示
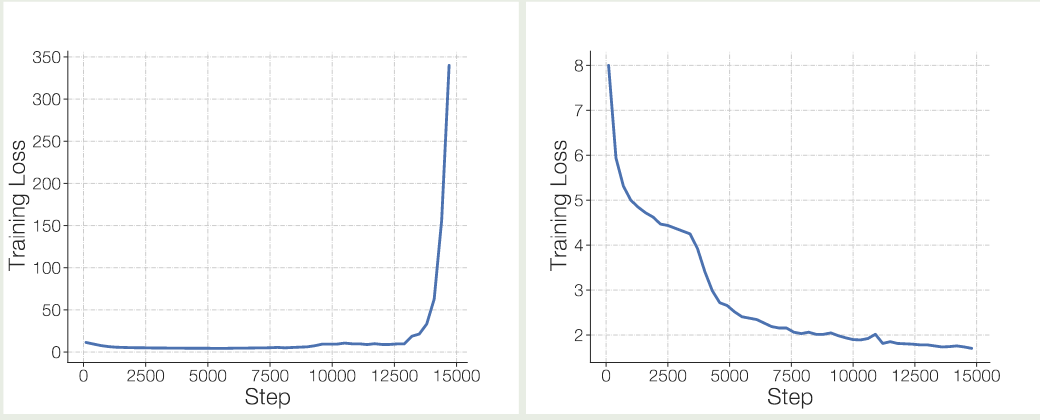
可以看到不同的实验,一次训练崩溃,一次训练正常。
作者接下来探究了如何提高训练的稳定性,作者有三点发现:
- 大多数方法都可以提高训练稳定性,但是也会是的模型表现更差
- router Z-loss 可以在不损失模型表现的情况下提高训练的稳定性
- multiplicative components 如 RMSNorm 等可以提高模型表现,但是训练稳定性更差
作者构建了一个 baseline 的 MoE 模型,总专家个数为 $N=32$, 激活专家个数为 $K=2$, Transformer block 按照 4 个 block 为一组,每组里包含一个 MoE layer. 为了避免初始化带来的误差,作者使用 6 个随机数种子进行训练。
Multiplicative Components
multiplicative components 指的是 GEGLU 和 RMSNorm 这些操作,其实验结果如下所示
| Method | Fraction Stable | Quality |
|---|---|---|
| Baseline | 4/6 | $-1.755 \pm0.02$ |
| Remove GEGLU | 3/3 | $-1.849 \pm0.02$ |
| Remove RMS Norm. Scale Param | 3/3 | $-2.020 \pm0.06$ |
结果发现,移除掉 multiplicative components 之后,模型训练变得稳定,但是效果也变差了。
Adding Noise
接下来作者尝试了 Switch Transformer 中的 jitter noise 和 dropoout 方法,实验结果如下图所示
| Method | Fraction Stable | Quality |
|---|---|---|
| Baseline | 4/6 | $-1.755 ± 0.02$ |
| Input jitter ($10^{-2}$) | 3/3 | $-1.777 \pm 0.03$ |
| Dropout (0.1) | 3/3 | $-1.822 \pm0.11$ |
实验结果显示,加入噪声对模型的表现存在负面影响。
Constraining Activations
作者接下来分析了以下 Switch Transformer 中 router 存在的问题,作者发现尽管在 router 中使用 float32 可以提高训练稳定性,但是这还不够,因此作者使用了如下的 router Z-loss:
其中 $B, N$ 分别是 batch size 和专家个数,$x_j^{(i)}$ 代表了第 $j$ 个专家对 $i$ 个 token 的激活 logits. 通过增加这个 loss, 我们可以让 routing layer 的 logits 都在一个合理的范围内。
| Method | Fraction Stable | Quality ($\uparrow$) | |
|---|---|---|---|
| Baseline | $4/6$ | $-1.755 \pm 0.02$ | |
| Update clipping (clip = 0.1) | $3/3$ | $-4.206 \pm 0.17$ | |
| Router Z-Loss | $3/3$ | $-1.741 \pm 0.02$ |
可以看到,加入 router Z-loss 之后,模型的稳定性和表现都有了提升。
因此,在本文中,作者使用的损失函数为
$$ \mathcal{L} = \mathcal{L}_{CE} + \alpha \mathcal{L}_B + \beta \mathcal{L}_z $$其中 $\mathcal{L}_{CE}, \mathcal{L}_B$ 分别是 cross-entropy loss 和 Load Balancing loss, $\alpha,\beta$ 是对应 loss 的权重。
Numerical Precision
接下来作者探究了数值精度对训练效率和稳定性的影响,作者发现使用低精度进行训练的优势有:
- 通信开销更小
- 计算消耗更小
- 内存需求更小
但是低精度进行训练的问题是存在严重的 roundoff error, 其示意图如下所示

Fine-tuning
作者在本节探究了如何 fine-tune 一个 MoE 模型。
作者首先通过实验给出了 MoE 模型容易过拟合的结论,实验结果如下图所示
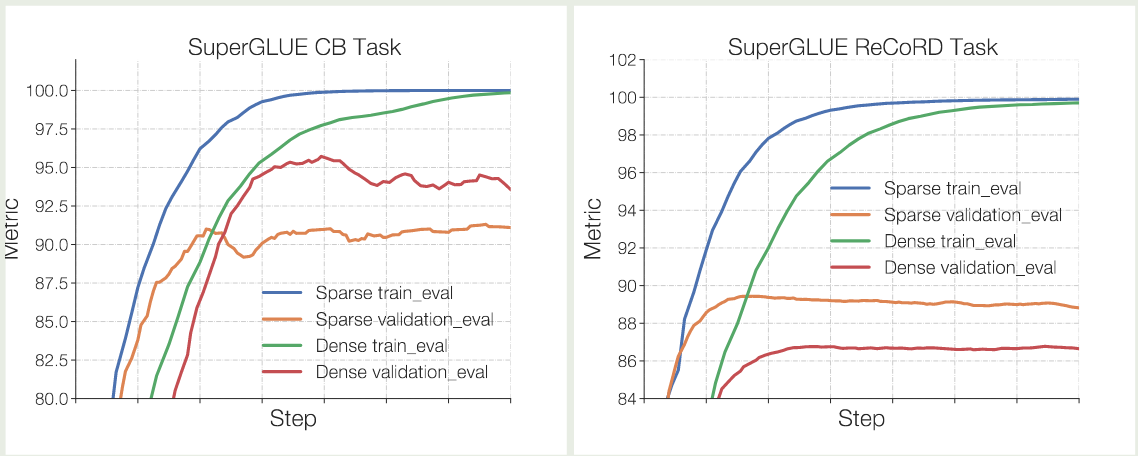
可以看到,在两个人呢误伤,MoE 模型相比于 dense 模型都更容易过拟合。
接下来作者探究了超参数特别是 batch size 和 learning rate 对模型表现的影响,结果如下图所示
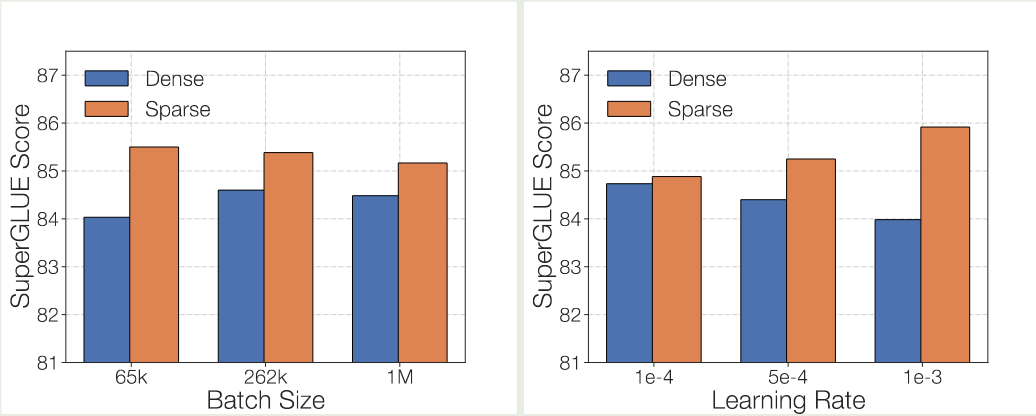
可以看到,与 dense 模型相反,MoE 模型需要更大的 batch size 以及更小的 learning rate.
Design Sparse Models
首先作者分析了专家个数 $N$ 的设置,作者认为当专家个数超过 $256$ 之后,带来的收益就微乎其微了。并且,当专家个数增加之后,虽然算力没有变化,但是通信开销以及计算优化会变得更加困难。作者还认为,在 TPU 上,每个 core 应该进放置一个 expert
作者还对 capacity factor 进行了实验,实验结果显示,提升 capacity factor 可以提高模型的表现。但是同时也会带来计算开销,从而让模型训练更慢,实验结果如下图所示
| Model | Train CF | Step Time (s) ($\downarrow$) | |
|---|---|---|---|
| ST-MoE-L | 1.25 | $2.397$ | |
| ST-MoE-L | 2.0 | $2.447 (+7\%)$ | |
| ST-MoE-32B | 1.25 | $4.244$ | |
| ST-MoE-32B | 2.0 | $4.819 (+14\%)$ |
最终结论如下:
- 使用 top-2 routing, 即激活 $K=2$ 个专家,capacity factor 设置为 $1.25$, 每个 core 上最多放置一个专家
- 在评估时可以动态调整 capacity factor
Tracing Tokens through the Model
在这一节里,作者分析了 MoE 模型专家的性质。
首先,作者发现,每一层里,至少有一个专家对于 sentinel token 比较敏感。并且,encoder 里的专家 specialization 更强,比如某些专家会负责 punctuation, verbs, proper names 等
接下来,作者发现,专家的 specialization 在 decoder 里几乎没有,作者认为这是因为 target token distribution 不同导致的,即:
- decoding 是只有一小部分 token 被一个专家处理
- decoding 过程中大部分 token 都是 sentinel token
因此,每个 group 相比于 encoder 来说通常只 cover 一小部分的 semantic space
encoder 和 decoder 专家的 specialization 实验结果如下
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 | Uniform (32-experts) | |
|---|---|---|---|---|---|---|---|
| Encoder | 2.2 | 1.8 | 1.6 | 1.7 | 1.7 | 1.2 | 3.5 |
| Decoder | 3.4 | 3.4 | 3.4 | 3.4 | 3.4 | 3.4 | 3.5 |
可以看到,decoder 的专家分布和均匀分布差不多,这说明 decoder 里的专家 specialization 更弱。
作者还探究了不同专家对于不同语言的敏感程度,结果发现,专家对于不同语言并没有出现明显的 specialization 现象,作者分析原因认为,输入一般只含有一种语言,因此各个专家均需要去处理对应语言的 token, 这就导致了专家对于不同语种的数据处理基本上没有太大差别。
Conclusion
在本文中,作者提出了 ST-MoE 系列 MoE 大语言模型,作者通过实验优化了 MoE 模型训练的不稳定性问题。